Проверка части с

Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь указанными критериями.

Начало формы

Задание С1 № 500407

а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку .

Решение.

а ) Запишем уравнение в виде:

Значит, или , откуда , , или , откуда , . б) С помощью числовой окружности (см. рис.) отберём корни, принадлежащие отрезку . Находим числа Ответ: а) , ; , ; б) .

Задание С2 № 500193

Точка  — середина ребра куба . Найдите площадь сечения куба плоскостью , если ребра куба равны 2.

Решение.

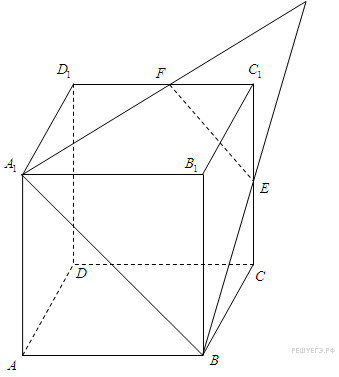Прямая пересекает прямую в точке . Прямая пересекает ребро в его середине — точке .  — сечение куба плоскостью . В равнобедренном треугольнике , и высота . Поскольку  — средняя линия треугольника , получаем:

Ответ: 4,5.

Задание С3 № 500963

Решите систему неравенств:

Решение.

Реши первое неравенство. Сделаем замену получаем

или

Обратная замена дает или Решим второе неравенство. Сделав замену получаем

Значит, Таким образом, получаем решение системы:

Ответ:

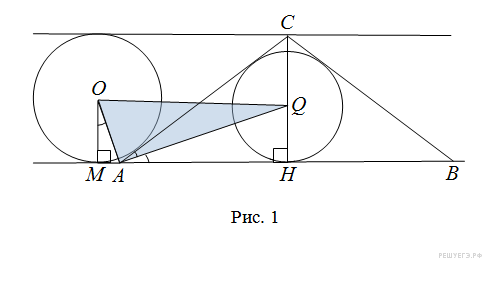
Задание С4 № 485970 Расстояние между параллельными прямыми равно 6. На одной из них лежит вершина C, на другой — основание AB равнобедренного треугольника ABC. Известно, что Найдите расстояние между центрами окружностей, одна из которых писана в треугольник ABC, а вторая касается данных параллельных прямых и боковой стороны треугольника ABC. Решение.

Пусть — высота треугольника, — радиус окружности, вписанной треугольник , — центр этой окружности. Так как, , то . Следовательно, полупериметр треугольника равен , а его площадь , откуда . Пусть . Тогда , , . Пусть окружность с центром касается данных параллельных прямых и боковой стороны равнобедренного треугольника , причем прямой — в точке , и не имеет общих точек с боковой стороной (рис. 1). Нетрудно понять, что радиус этой окружности равен 3. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому — биссектриса угла MAC . Тогда

, , , .

Из прямоугольного треугольника находим, что

.

Пусть теперь окружность с центром касается данных параллельных прямых и боковой cтороны равнобедренного треугольника , причем прямой — в точке , и пересекает боковую сторону (рис. 2). Тогда точки O и Q лежат на биссектрисе угла . Треугольник подобен треугольнику с коэффициентом , поэтому

.

Следовательно, Ответ: или

Задание С5 № 484628 Найдите все значения a при каждом из которых система 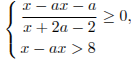не имеет решений.

Решение.

Рассмотрим второе неравенство системы .

Если , то неравенство, а значит, и система не имеет решений. Если , то решение неравенства — луч .

Если , то решение неравенства — луч .

При первое неравенство системы принимает вид

Если , то решение этой системы — два луча с концами в точках .

Если , то решение этой системы — полуинтервал с концами в точках .

Отметим, что точки нет в множестве решений второго неравенства. Для того, чтобы система не имела решений, при необходимо и достаточно:

.

Ответ: .

Задание С6 № 485960

В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2076. а) может ли в последовательности быть три члена? б) может ли в последовательности быть четыре члена? в) может ли в последовательности быть меньше 2076 членов?

Решение.

а) Нет, поскольку не делится на 2, а не является квадратом натурального числа. б) Последовательность не может быть арифметической прогрессией, поскольку не делится на 3. Последовательность не может быть геометрической прогрессией, поскольку не является кубом натурального числа. Если первые три члена образуют геометрическую прогрессию, а последние три – арифметическую, то эти числа: но уравнение не имеет целых корней. Если первые три члена образуют арифметическую прогрессию, а последние три – геометрическую, то эти числа: и где — натуральное число. Тогда последнее число должно равняться

но это не натуральное число. в) Да, например,