Результаты Вариант № 399

№ п/п	Номер	Тип		Правильный ответ
1	77338	B1		21
2	26871	B2		11
3	27722	B3		4,5
4	41055	B4		15900
5	26653	B5		4
6	27812	B6		60
7	26777	B7		1
8	317540	B8		7
9	910	B9		13
10	320205	B10		0,125
11	27168	B11		4
12	43097	B12		3,5
13	99575	B13		100
14	26699	B14		32

Решения

↑ Задание 1 № 77338 тип B1

В общежитии института в каждой комнате можно поселить четырех человек. Какое наименьшее количество комнат необходимо для поселения 83 иногородних студентов? Решение. Разделим 83 на 4: . Значит, для поселения 83 иногородних студентов необходима 21 комната.

Ответ: 21.

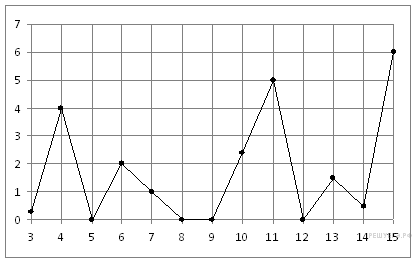↑ Задание 2 № 26871 тип B2

На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало миллиметров осадков.

Решение. Из графика видно, впервые 5 мм осадков выпало 11 февраля (см. рисунок).

Ответ: 11.

↑ Задание 3 № 27722 тип B3

Стороны правильного треугольника равны 3. Найдите скалярное произведение векторов  и . Решение. Скалярное произведение двух векторов равно произведению их длин на косинус угла между ними. Углы в правильном треугольнике равны . Поэтому скалярное произведение равно . Ответ: 4,5.

↑Задание 4 № 41055 тип B4

При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 13 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1450 рублей, щебень стоит 700 рублей за тонну, а мешок цемента стоит 220 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?

Решение. Рассмотрим два варианта. Стоимость каменного фундамента складывается из стоимости камня 9   1450 = 13 050 руб., а также стоимости цемента 13   220 = 2860 руб. Всего 2860 + 13 050 = 15 910 руб. Стоимость бетонного фундамента складывается из стоимости цемента 50   220 = 11 000 руб., а также стоимости щебня 7   700 = 4900 руб. Всего 4 900 + 11 000 = 15 900 руб. Стоимость самого дешевого варианта составляет 15 900 рублей.

Ответ: 15 900.

↑ Задание 5 № 26653 тип B5 Найдите корень уравнения . Решение. Перейдем к одному основанию степени:

. Ответ: 4.

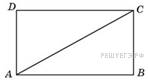↑ Задание 6 № 27812 тип B6

Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, которые образует диагональ со сторонами прямоугольника? Ответ выразите в градусах. Решение. диагональ прямоугольника является гипотенузой прямоугольного треугольника. Так как она вдвое больше одной из сторон прямоугольника, являющейся катетом того же треугольника, то угол, лежащий против этой стороны, равен . Больший угол равен .

Ответ: 60.

↑ Задание 7 № 26777 тип B7 Найдите , если и . Решение. Поскольку угол лежит в четвертой четверти, его косинус положителен. Поэтому

.Ответ: 1.

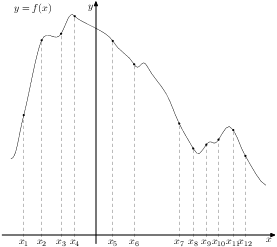
↑ Задание 8 № 317540 тип B8 На рисунке изображён график функции и двенадцать точек на оси абсцисс: , , , , . В скольких из этих точек производная функции отрицательна?

Решение. Отрицательным значениям производной соответствуют интервалы, на которых функция убывает. В этих интервалах лежат точки Таких точек 7. Ответ:7.

↑ Задание 9 № 910 тип B9 (решено неверно или не решено)

Высота конуса равна 12, а диаметр основания – 10. Найдите образующую конуса. Решение. образующая конуса по теореме Пифагора равна

Ответ: 13.

↑Задание 10 № 320205 тип B10

Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5 = 0,125.

Ответ: 0,125.

↑ Задание 11 № 27168 тип B11

Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба? Решение. По условию , откуда Площади их поверхностей соотносятся как .

Ответ: 4.

↑Задание 12 № 43097 тип

Водолазный колокол, содержащий в начальный момент времени  моля воздуха объeмом  л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма . Работа, совершаемая водой при сжатии воздуха, определяется выражением  (Дж), где постоянная, а  К — температура воздуха. Какой объeм (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 27 840 Дж?

Решение. Задача сводится к решению уравнения при заданных значениях постоянной , температуры воздуха К, количества воздуха моль и объема воздуха  л:

л.

Значит, объем, который будет занимать воздух, равен 3,5 л.

Ответ: 3,5.

↑ Задание 13 № 99575 тип B13

Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Решение. Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:

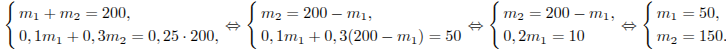
Таким образом, первый сплав легче второго на 100 килограммов.

Ответ: 100.

↑ Задание 14 № 26699 тип B14

Найдите наибольшее значение функции на отрезке Решение. Найдем производную заданной функции: Уравнение не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей.

Следовательно, наибольшим значением функции на заданном отрезке является

Ответ: 32.