Результаты Вариант № 278

№ п/п	Номер	Тип		Правильный ответ
1	500028	B1		60
2	27527	B2		14
3	27594	B3		6
4	26683	B4		2,5
5	26669	B5		-4
6	27282	B6		4
7	26760	B7		-16
8	27491	B8		-3
9	908	B9		17
10	285925	B10		0,36
11	27191	B11		36
12	319859	B12		35
13	99618	B13		9
14	245179	B14		2

Решения

↑ Задание 1 № 500028 Летом килограмм клубники стоит 80 рублей. Маша купила 1 кг 750 гр клубники. Сколько рублей сдачи она должна получить с 200 рублей? Решение. Найдем стоимость покупки: 1 кг 750 г клубники стоят рублей. Значит, с 200 рублей Маша получит  рублей сдачи. Ответ: 60.

↑ Задание 2 № 27527 На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.

Р ешение. Из 16 наблюдений, представленных на графике, 2 дня выпадало более 3 мм осадков. Поэтому 14 дней выпадало менее 3 мм осадков. Ответ: 14.

↑

Задание 3 № 27594 Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции. Решение. Площадь трапеции равна произведению полусуммы оснований на высоту. Средняя линия трапеции равна полусумме оснований. Поэтому см². Ответ: 6.

↑ Задание 4 № 26683

И з пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 35 км/ч, через пункт С едет автобус со средней скоростью 30 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 40 км/ч. На рисунке показана схема дорог и расстояние между пунктами по дорогам. Все три автомобиля одновременно выехали из А. Какой автомобиль добрался до D позже других? В ответе укажите, сколько часов он находился в дороге. Решение. Рассмотрим все варианты. Грузовик, идущий через пункт B, прошел путь 28 + 42 = 70 км потратил на дорогу 70 : 35 = 2 часа. Автобус, идущий через пункт C, прошел путь 45 + 30 = 75 км потратил на дорогу 75 : 30 = 2,5 часа. Автомобиль, идущий без промежуточных пунктов, прошел путь 60 км потратил на дорогу 60 : 40 = 1,5 часа. Позже других добрался автобус. Ответ: 2,5.

↑ Задание 5 № 26669 Найдите корни уравнения: В ответе запишите наибольший отрицательный корень. Решение. Последовательно получаем:

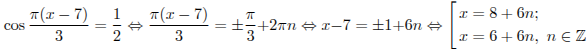
Значениям соответствуют положительные корни. Если , то и . Если , то и . Значениям соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число . Ответ: −4.

↑ Задание 6 № 27282 тип B6

В треугольнике угол равен 90°, – высота, , .

Найдите . Решение.

. Ответ: 4.

↑ Задание 7 № 26760 Найдите значение выражения . Решение. Выполним преобразования:

Ответ: -16.

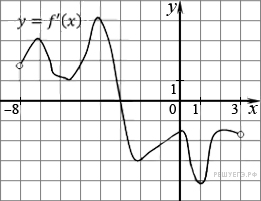↑ Задание 8 № 27491

На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка функция принимает наибольшее значение?

Решение. На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наибольшее значение функции достигается на левой границе отрезка, т. е. в точке −3.

Ответ: −3.

↑ Задание 9 № 908 Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса. Решение. образующая конуса по теореме Пифагора равна

Ответ: 17.

↑ Задание 10 № 285925

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Решение. В первом туре Руслан Орлов может сыграть с 26 − 1 = 25 бадминтонистами, из которых 9 — из России. Значит вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна

Ответ: 0,36.

↑ Задание 11 № 27191

Н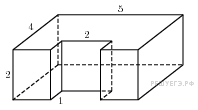 айдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). Решение. Объем данного многогранника равен разности объемов параллелепипедов со сторонами 5, 2, 4 и 1, 2, 2:

. Ответ: 36.

↑Задание 12 № 319859

Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности , оперативности , объективности публикаций , а также качества сайта . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.

Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид

Каким должно быть число , чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1? Решение. Поскольку показатели максимальны, они равны 5. Подставим значения в формулу:

Ответ:35

↑ Задание 13 № 99618

Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба? Решение. Пусть объем бассейна равен 1. Обозначим и — скорости наполнения бассейна первой и второй трубой, соответственно. Две трубы наполняют бассейн за 3 часа 36 минут:

. По условию задачи одна первая труба наполняет бассейн за 6 часов, то есть . Таким образом, .

Тем самым, вторая труба за час наполняет 1/9 бассейна, значит, вторая труба наполняет этот бассейн за 9 часов. Ответ: 9.

Приведем другое решение. Первая труба за час наполняет 1/6 бассейна, значит, за 3 ч 36 мин = 3,6 часа она заполнит 0,6 бассейна. Следовательно, вторая труба за 3,6 часа заполнит 0,4 бассейна. Поэтому весь бассейн она заполнит за время 3,6:0,4 = 9 часов.

↑ Задание 14 № 245179 Найдите наименьшее значение функции . Решение. Квадратный трехчлен с положительным старшим коэффициентом достигает наименьшего значения в точке , в нашем случае — в точке 3. Функция в этой точке определена и принимает значение . Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции.

Ответ: 2.

Начало формы

Задание С1 № 485964 а) Решите уравнение . б) Укажите корни этого уравнения, принадлежащие промежутку

Решение.

а) Преобразуем уравнение:

. Если , то из уравнения следует , что невозможно. Значит, на множестве корней уравнения . Разделим обе части уравнения на :

.

б) Составим двойное неравенство: , откуда . Следовательно, . Поэтому на данном отрезке получаем единственный корень .

Ответ: а) ; б) .

Вопрос: скажите, пожалуйста, почему sinX=0 невозможно?

Ответ: Одновременно sin(x) и cos(x) не могут равняться 0.

Задание С2 № 500387

На ребре куба отмечена точка так, что . Найдите угол между прямыми и .

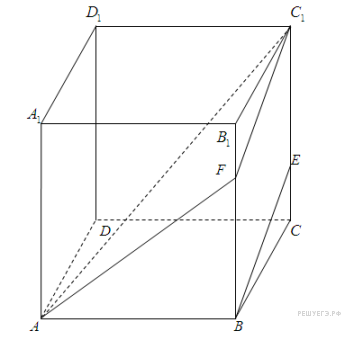
Решение. Примем ребро куба за единицу. Тогда . Поскольку , получаем: и . Проведем через точку прямую, параллельную . Она пересекает ребро в точке , причем треугольники и равны. Искомый угол равен углу (или смежному с ним). В прямоугольном треугольнике с прямым углом В прямоугольном треугольнике с прямым углом

В треугольнике

откуда , тогда

Ответ может быть представлен и в другом виде: или Ответ: .

Задание С3 № 484586

Решите неравенство .

Решение.

. Сделав замену переменной , получаем:

1) 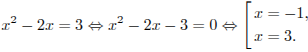2) 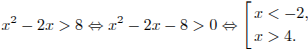Ответ: .

Вопрос:На основании каких законов мы после замены перешли от неравенства с логарифмами к системе без логарифмов: второе неравенство в системе понятно - оно из области допустимых значений, а вот как в первом избавились от логарифмов - не понятно?

Служба поддержки:

Здесь применена теорема: на ОДЗ знак разности совпадает со знаком произведения .

    Задание С4 № 485995

Дан треугольник со сторонами и На стороне взята точка , а на отрезке — точка , причем и Окружность с центром проходит через точку . Найдите расстояние от точки до точки пересечения этой окружности с прямой

РешениЕ.П роведем через вершину прямую, параллельную Пусть — точка ее пересечения с прямой а — точка пересечения и Треугольник подобен треугольнику с коэффициентом поэтому Значит, треугольник равен треугольнику по стороне и двум прилежащим к ней углам. Тогда — середина Следовательно, — медиана треугольника Через вершину проведем прямую, параллельную Пусть   — точка ее пересечения с прямой Треугольник подобен треугольнику с коэффициентом поэтому Тогда треугольники и равны по стороне и двум прилежащим к ней углам. Поэтому  — середина Окружность с центром проходит через точку , и при этом Следовательно, — радиус этой окружности. Треугольник прямоугольный, а точка — одна из точек пересечения прямой и окружности. Пусть — вторая точка пересечения окружности с прямой Тогда угол — вписанный и опирающийся на диаметр так что то есть — высота треугольника Отсюда

Ответ: 12,5 или 6,72.

Задание С5 № 484649 Найдите все положительные значения а, при каждом из которых система имеет единственное решение.

Решение.

Если , то уравнение задает окружность с центром в точке радиуса 2, а если , то оно задаёт окружность с центром в точке того же радиуса (см. рис.).

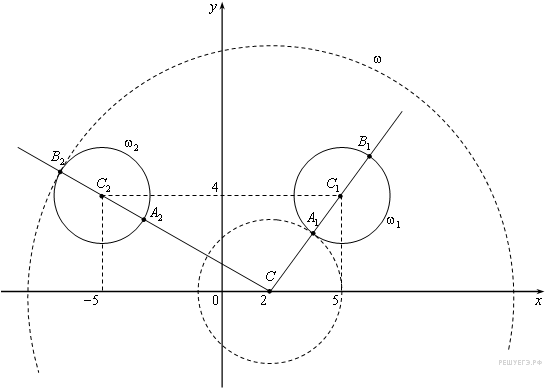
При положительных значениях параметра а уравнение задаст окружность с центром в точке радиуса а. Поэтому задача состоит в том, чтобы найти все значения параметра а, при каждом из которых окружность имеет единственную общую точку с объединением окружностей и . Из точки С проведём луч и обозначим и точки его пересечения с окружностью , где лежит между С и . Так как , то

, .

При или окружности и не пересекаются. При окружности и имеют две общие точки. При или окружности и касаются. Из точки С проведём луч и обозначим и точки его пересечения с окружностью , где лежит между точками и . Так как , то

, . При или окружности и не пересекаются. При окружности и имеют две общие точки. При или окружности и касаются. Исходная система имеет единственное решение тогда и только тогда, когда окружность касается ровно одной из двух окружностей и и не пересекается с другой. Так как , то условию задачи удовлетворяют только числа и . Ответ: 3; .

Задание С6 № 500005

На доске написано число 7. Раз в минуту Вася дописывает на доску одно число: либо вдвое большее какого-то из чисел на доске, либо равное сумме каких-то двух чисел, написанных на доске (таким образом, через одну минуту на доске появится второе число, через две ― третье и т.д.). а) Может ли в какой-то момент на доске оказаться число 2012? б) Может ли в какой-то момент сумма всех чисел на доске равняться 63? в) Через какое наименьшее время на доске может появиться число 784?

Решение.

а) Заметим, что каждое число на доске будет делиться на 7. Действительно, исходное число делится на 7, в случае удвоения числа делящегося на 7, получится число, делящееся на 7. А при сложении чисел, делящихся на 7, также получится число, делящееся на 7. Таким образом, все числа на доске будут делиться на 7, а 2012 на 7 не делится, следовательно, оно не может появиться на доске. б) Да, может. Пример: 7, 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7). Сумма полученных 5 чисел равна 63. Замечание. В условии не сказано, что одно число нельзя удваивать несколько раз. в) Как было замечено в пункте а, все числа на доске будут делиться на 7. Рассмотрим аналогичную задачу, разделив исходное число 7 и то число, которое нужно получить, т.е. 784, на 7. От этого количество операций не изменится. Таким образом, достаточно за наименьшее количество операций получить число 112, начав с числа 1. Заметим, что наибольшее число, которое может получиться на доске через 6 минут, равно 64 (если Вася каждый раз будет удваивать текущее наибольшее число). Следовательно, если в первые 6 минут Вася каждый раз удваивал наибольшее число на доске, то число 112 нельзя получить за 7 минут: если число 64 удвоить, то получится 128, а если прибавить к нему число, не превосходящее 32, то 112 не получится. В том случае, если в течение первых 6 минут Вася использовал хотя бы одно сложение вместо удвоения, то при первом использовании сложения наибольшее число, записанное на доске увеличилось не более, чем в полтора раза: действительно, в этом случае самый большой результат получится тогда, когда мы к максимальному на данный момент числу прибавим второе по величине, то есть, его половину (напомним, что мы рассматриваем первый случай сложения, то есть до этого были только удвоения). Таким образом, даже если в течение первых 7 минут сделано 6 удвоений и одно сложение (в некотором порядке), то наибольшее число, которое может получиться, равно , что меньше 112. Итак, за 7 минут число 112 получить невозможно. Приведем пример, как его получить за 8 минут: 1 1,2 1,2,4 1,2,4,8 1,2,4,8,16 1,2,4,8,16,32 1,2,4,8,16,32,64 1,2,4,8,16,32,64,96 (96 = 64 + 32 ) 1,2,4,8,16,32,64,96,112 (112 = 96 + 16 ).

Ответ: а) нет; б) да; в) 8 минут