Задание с6 № 484654

Перед каждым из чисел 14, 15, . . ., 20 и 4, 5, . . ., 8 прозвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 35 полученных результатов складывают. Какую наименьшую по модулю и какую нибольшую сумму можно получить в итоге?

Решение.

1. Если все числа первого набора взяты с плюсами, а второго — с минусами, то сумма максимальна и равна

.

2. Так как предыдущая сумма оказалась нечетной, то число нечетных слагаемых в ней — нечетно, причем это свойство всей суммы не меняется при изменении знака любого ее слагаемого. Поэтому любая из полученны сумм будет не четной, а значит, не будет равна 0. 3. Значение 1 сумма принимает, например, при следующей расстановке знаков у чисел:

.

Ответ: 1 и 805.

Вариант № 1941368

№ п/п	Номер	Тип	Правильный ответ
1	77365	B1	190
2	500138	B2	9
3	27602	B3	18
4	26675	B4	1840
5	26655	B5	12,5
6	27225	B6	0,96
7	26844	B7	28
8	27500	B8	6
9	925	B9	3
10	320186	B10	0,33
11	27042	B11	0,25
12	27977	B12	18
13	99585	B13	22
14	26716	B14	-18

↑ Задание 1 № 77365 тип B1

Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 200 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу? Решение. Скидка на покупку составит 200   0,05 = 10 рублей. Значит, держатель дисконтной карты заплатит за книгу 200 − 10 = 190 рублей.

Ответ: 190.

↑ Задание 2 № 500138 тип B2 (решено неверно или не решено)

На диаграмме показана среднемесячная температура воздуха (в градусах Цельсия) в Кемерово по результатам многолетних наблюдений. Найдите по диаграмме количество месяцев, когда среднемесячная температура в Кемерово выше минус 10 градусов Цельсия.

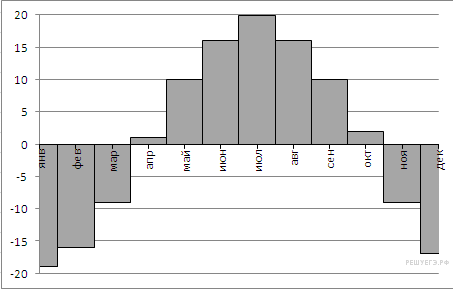
Решение. Из диаграммы видно, что среднемесячная температура воздуха в Кемерово ниже −10 градусов Цельсия в январе, феврале и декабре, а в остальные месяцы она выше.

↑ Задание 3 № 27602 тип B3

Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2. Решение. Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Периметр будет соответственно равен P = 2   a + 2   2a = 18, тогда одна из сторон равна 3, а другая 6. Поэтому S = 3   6 = 18.

Ответ: 18.

↑ Задание 4 № 26675 тип B4

Для остекления музейных витрин требуется заказать 20 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25 м². В таблице приведены цены на стекло и на резку стекол. Сколько рублей будет стоить самый дешевый заказ?

Фирма	Цена стекла (руб. за 1 м2)	Резка стекла (руб. за одно стекло)	Дополнительные условия
A	300	17
Б	320	13
В	340	8	При заказе на сумму больше 2500 руб. резка бесплатно.

Решение. Общая площадь стекла, которого нужно изготовить равна 20   0,25 = 5 м². Стоимость заказа в фирме А складывается из стоимости стекла 300   5 = 1500 руб. и стоимости его резки и шлифовки 17   20 = 340 руб. Всего 1840 руб. Стоимость заказа в фирме Б складывается из стоимости стекла 320   5 = 1600 руб. и стоимости его резки и шлифовки 13   20 = 260 руб. Всего 1860 руб. Стоимость заказа в фирме В складывается из стоимости стекла 340   5 = 1700 руб. и стоимости его резки и шлифовки 8   20 = 160 руб. Всего 1860 руб. Стоимость самого дешевого заказа составляет 1840 рублей. Ответ: 1840.

Вопрос: объясните, пожалуйста, разве надо не лист квадрата в 1 кв. м. разрезать на 4 части? На первый взгляд кажется, что нужно купить 5 квадратных листов стекла по 1 квадратному метру и разрезать их по числу стёкол.

Ответ: Стекла (обои, линолеум, деревянные панели, другие отделочные и строительные материалы) в виде квадратных листов обычно не производятся и не продаются. Хотя цена на эти товары зависит от их площади в квадратных метрах.

↑ Задание 5 № 26655 тип B5 Найдите корень уравнения . Решение. Перейдем к одному основанию степени:

.Ответ: 12,5.

↑ Задание 6 № 27225 тип B6

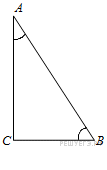
В треугольнике угол равен 90°, . Найдите . Решение.

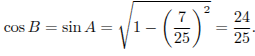
Ответ: 0,96.

↑ Задание 7 № 26844 тип B7 Найдите значение выражения . Решение. Выполним преобразования: . Ответ: 28.

↑ Задание 8 № 27500 тип B8

На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. 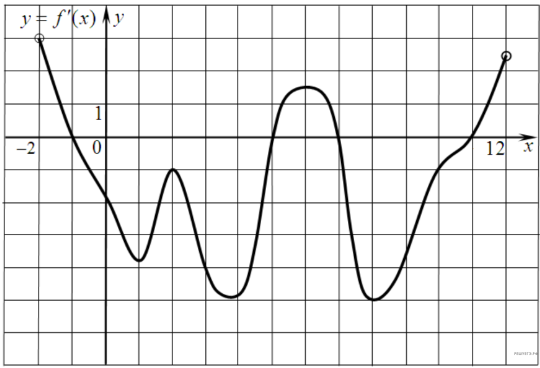Решение. Промежутки убывания функции f(x) соответствуют промежуткам, на которых производная функции отрицательна, то есть интервалам (−1; 5) длиной 6 и (7; 11) длиной 4. Длина наибольшего из них 6. Ответ: 6.

↑ Задание 9 № 925 тип B9 Площадь боковой поверхности цилиндра равна 21 , а диаметр основания равен 7. Найдите высоту цилиндра. Решение. высота цилиндра равна

О твет: 3.

↑ Задание 10 № 320186 тип B10 На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых. Решение. Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (Д — Дания, Ш — Швеция, Н — Норвегия):

...Д...Ш...Н..., ...Д...Н...Ш..., ...Ш...Н...Д..., ...Ш...Д...Н..., ...Н...Д...Ш..., ...Н...Ш...Д...

Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна Ответ: 0,33.

Замечание. Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из предыдущих групп: оно равно Общее количество перестановок из всех групп равно Поэтому искомая вероятность равна

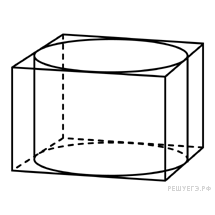
↑ Задание 11 № 27042 тип B11

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра. Решение.Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна . Ответ: 0,25.

↑ Задание 12 № 27977 тип B12

Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой (в килограммах) от температуры до температуры (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы кг. Он определяется формулой , где Дж/(кг К) – теплоёмкость воды, Дж/кг – удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть кг воды от до кипения, если известно, что КПД кормозапарника не больше . Ответ выразите в килограммах. Решение.Задача сводится к решению неравенства %. А при известных значениях теплоёмкости воды Дж/кг, удельной теплоты сгорания дров Дж/кг, массы воды кг и изменения температуры К:

кг. Ответ: 18.

↑ Задание 13 № 99585 тип B13

Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней. Решение. В первый день Вера подписала открыток, во второй – , …, в последний – открыток. Всего было подписано открыток. Количество подписываемых открыток увеличивалось на каждый день.

.

Тогда за четвертый день было подписано

открыток.

Ответ: 22.

↑ Задание 14 № 26716 тип B14 Найдите наименьшее значение функции на отрезке .Решение.Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

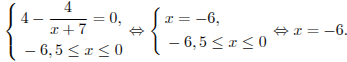
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

. Ответ: −18.

Начало формы