Задание с1 № 500638

а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие промежутку .

Решение.

а) Решим уравнение:

б) Отбор корней. Составим двойное неравенство:

Тогда искомый корень . Ответ: а) ; б) .

Задание с2 № 485955

В правильной шестиугольной призме все рёбра которой равны 10, найдите расстояние от точки до прямой

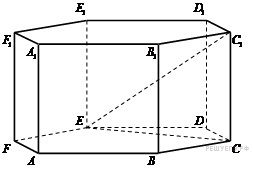
Решение.

Так как — правильный шестиугольник, прямые и перпендикулярны. Поскольку прямые и параллельны, перпендикулярно Тогда по теореме о трёх перпендикулярах перпендикулярна , поэтому длина отрезка равна искомому расстоянию. По условию диагональ правильного шестиугольника . Тогда по теореме Пифагора для треугольника находим, что Ответ: 20.

Задание с3 № 500409

Решите систему неравенств

.

Решение.

1. Решим первое неравенство системы. Сделаем замену , .

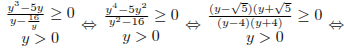
откуда находим: <math0; . Тогда или , откуда находим решение первого неравенства системы: ; . 2. Решим второе неравенство системы: . Рассмотрим два случая. Первый случай: .

откуда находим: . Учитывая условие , получаем: . Второй случай:

. Учитывая условие , получаем: . Решение второго неравенства исходной системы:

. 3. Поскольку , получаем решение исходной системы неравенств:

Ответ: ; ; ; .</math0

Задание с4 № 484613

Основание равнобедренного треугольника равно 40, косинус угла при вершине равен . Две вершины прямоугольника лежат на основании треугольника, а две другие — на боковых сторонах. Найдите площадь прямоугольника, если известно, что одна из его сторон вдвое больше другой.

Решение.

Пусть вершины K и L прямоугольника KLMN лежат на основании BC равнобедренного треугольника (точка K — между B и L), а вершины M и N — на боковых сторонах M и N соответственно. Обозначим

, .

Тогда

, .

Предположим, что сторона KL прямоугольника вдвое больше его стороны KN Положим Из прямоугольного треугольника BKN находим, что Тогда а так как , то

,

Откуда . Тогда . Следовательно,

.

Пусть теперь сторона KN прямоугольника вдвое больше его стороны KL. Положим . Из прямоугольного треугольника находим, что . Тогда , а так как KN=MN=y, то

,

откуда . Тогда . Следовательно, .

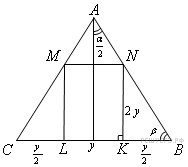
Ответ: 512 или 800.

Задание с5 № 484644

Найти все значения а, при каждом из которых функция имеет более двух точек экстремума.

Решение.

1. Функция f имеет вид а) при : , поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии ; б) при : , поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии . Все возможные виды графиков функции показаны на рисунках:

Графики обеих квадратичных функции проходят через точку . 3. Функция имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1):

.

Ответ: ; .