Вариант № 1941093

№ п/п	Номер	Тип		Правильный ответ
1	26617	B1		12
2	263737	B2		28
3	245006	B3		1
4	77359	B4		10100
5	315119	B5		7
6	27776	B6		40
7	26817	B7		-0,5
8	323077	B8		10
9	245359	B9		50
10	320179	B10		0,3
11	27081	B11		27
12	27959	B12		50
13	99598	B13		59
14	77435	B14		2

↑ Задание 1 № 26617 тип B1

Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды? Решение. Всего на теплоходе 775 человек. Разделим 775 на 70: .

Значит, на судне должно быть шлюпок. Ответ: 12.

↑ Задание 2 № 263737 тип B2 На рисунке жирными точками показана цена палладия, установленная Центробанком РФ во все рабочие дни в октябре 2008 года. По горизонтали указываются числа месяца, по вертикали — цена палладия в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей ценой палладия за указанный период. Ответ дайте в рублях за грамм.

Решение. Из графика видно, что наибольшая и наименьшая цены за указанный период составили 172 рубля и 144 рубля соответственно (см. рисунок). Их разность равняется 28 рублям.

Ответ: 28.

↑ Задание 3 № 245006 тип B3

Н айдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Решение. Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому

.

Примечание. Четырёхугольник составлен из двух треугольников, имеющих общее основание, равное длине квадратной клетки: прямоугольного с катетами 1 и 1, и тупоугольного с основанием длины 1 и высотой, проведенной к этому основанию, также длины 1. Поэтому площадь четырехугольника равна 0,5 + 0,5 = 1.

↑ Задание 4 № 77359 тип B4

В магазине одежды объявлена акция: если покупатель приобретает товар на сумму свыше 10 000 руб., он получает сертификат на 1000 рублей, который можно обменять в том же магазине на любой товар ценой не выше 1000 руб. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель И. хочет приобрести пиджак ценой 9500 руб., рубашку ценой 800 руб. и галстук ценой 600 руб. В каком случае И. заплатит за покупку меньше всего: 1) И. купит все три товара сразу. 2) И. купит сначала пиджак и рубашку, галстук получит за сертификат. 3) И. купит сначала пиджак и галстук, получит рубашку за сертификат. В ответ запишите, сколько рублей заплатит И. за покупку в этом случае. Решение. Рассмотрим все случаи. 1) При покупке всех трёх товаров покупатель И. потратит 9500 + 800 + 600 = 10 900 руб. 2) При покупке пиджака и рубашки покупатель И. потратит 9500 + 800 = 10 300 руб. Поскольку эта сумма больше 10 000, галстук будет приобретён за сертификат. В этом случае покупатель потратит 10 300 руб. 3) При покупке пиджака и галстука покупатель И. потратит 9500 + 600 руб. = 10 100 руб. Поскольку эта сумма больше 10 000, рубашка будет приобретена за сертификат. В этом случае покупатель потратит 10 100 руб. В третьем случае покупатель потратит меньше всего — 10 100 рублей.

ответ: 10100

↑ Задание 5 № 315119 тип B5 Найдите корень уравнения . Решение. Если две дроби с равным числителем равны, то равны их знаменатели. Имеем

Ответ:7.

↑ Задание 6 № 27776 тип B6

В треугольнике угол равен , угол равен ,  — биссектриса,  — такая точка на , что . Найдите угол . Ответ дайте в градусах. Решение. треугольники и равны по двум сторонам и углу, лежащему между ними, значит, . Тогда

. Ответ: 40.

↑ Задание 7 № 26817 тип B7 Найдите значение выражения при . Решение. Выполним преобразования:

Ответ: -0,5.

↑ Задание 8 № 323077 тип B8

На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].

Решение. По определению первообразной на интервале (−3; 5) справедливо равенство

Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на отрезке [−2;4] лежат 10 точек. Таким образом, на отрезке [−2;4] уравнение имеет 10 решений.

Ответ:10.

↑ Задание 9 № 245359 тип B9

Найдите квадрат расстояния между вершинами C и A₁ прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA₁=3. Решение. Рассмотрим прямоугольный треугольник в котором является гипотенузой. По теореме Пифагора

В прямоугольнике   – диагональ, = . Значит,

Ответ: 50.

↑ Задание 10 № 320179 тип B10 Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три? Решение. Натуральных чисел от 10 до 19 десять, из них на три делятся три числа: 12, 15, 18. Следовательно, искомая вероятность равна 3:10 = 0,3. Ответ: 0,3.

↑ Задание 11 № 27081 тип B11 Во сколько раз увеличится объем куба, если его ребра увеличить в три раза? Решение. Объем куба с ребром равен . Если ребра увеличить в раза, то объем куба увеличится в раз.

Ответ: 27.

↑ Задание 12 № 27959 тип B12

В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону где – время в секундах, прошедшее с момента открытия крана, – начальная высота столба воды, – отношение площадей поперечных сечений крана и бака, а – ускорение свободного падения (считайте м/с ). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды? Решение. Формулой, описывающей уменьшение высоты столба воды с течением времени, является

Четверть первоначального объёма воды в баке останется, когда высота столба воды будет 5 м. Определим требуемое на вытекание трех четвертей воды время — найдем меньший корень уравнения :

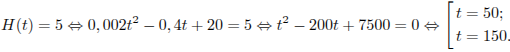
Таким образом, через 50 секунд после открытия крана в баке останется четверть первоначального объёма воды. Ответ: 50.

Вопрос: почему именно ответ 50 секунд, а не 150? Я часто теряюсь, когда встречаюсь с таким решением.

Ответ: Потому, что вся вода выльется ещё до того, как пройдет 150 секунд.

 

↑ Задание 13 № 99598 тип B13 Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. Решение. Пусть скорость второго автомобиля равна км/ч. За 2/3 часа первый автомобиль прошел на 14 км больше, чем второй, отсюда имеем

. Ответ: 59.

↑ Задание 14 № 77435 тип B14 Найдите точку максимума функции . Решение. Найдем производную заданной функции: . Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума . Ответ: 2.

Начало формы