Задание с1 № 500131

а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку .

Решение.

а) Запишем уравнение в виде

Значит, , откуда или . б) С помощью числовой окружности отберём корни, принадлежащие отрезку . Получим числа: ; ; . Ответ: а) , ; б) ; ; .

Задание с2 № 500588

В правильной четырёхугольной призме стороны основания равны 1, а боковые рёбра равны . На ребре отмечена точка так, что . Найдите угол между плоскостями и . Решение.

Прямая пересекает прямую в точке . Плоскости и пересекаются по прямой . Из точки опустим перпендикуляр на прямую , тогда отрезок (проекция ) перпендикулярен прямой . Угол является линейным углом двугранного угла, образованного плоскостями и . Поскольку , получаем:

Из подобия треугольников и находим:

В прямоугольном треугольнике с прямым углом : ; ; , откуда высота

.

Из прямоугольного треугольника с прямым углом получаем:

.

Ответ: .

Задание с3 № 484579

Решите неравенство .

Решение.

Пусть тогда неравенство принимает вид:

.

Так как , то , а значит, . Получаем:

.

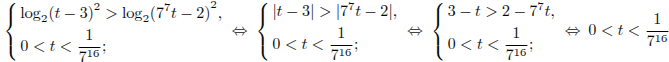Поясним: неравенство эквивалентно неравенству и выполнено для всех значений переменной. Итак,

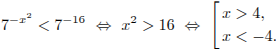
Ответ: .

Задание с4 № 485990

Дан треугольник со сторонами и На стороне взята точка а на отрезке — точка причем и Окружность с центром проходит через точку Найдите расстояние от точки до точки пересечения этой окружности с прямой

Решение.

Проведем через вершину прямую, параллельную . Пусть  — точка ее пересечения с прямой а  — точка пересечения и Треугольник подобен треугольнику с коэффициентом поэтому Значит, треугольник равен треугольнику по стороне и двум прилежащим к ней углам. Тогда — середина стороны Следовательно, — медиана треугольника Через вершину проведем прямую, параллельную Пусть — точка ее пересечения с прямой Треугольник подобен треугольнику с коэффициентом поэтому Тогда треугольники и равны по стороне и двум прилежащим к ней углам. Поэтому — середина   Окружность с центром проходит через точку и при этом Следовательно, — радиус этой окружности. Треугольник прямоугольный, а точка — одна из точек пересечения прямой и окружности. Пусть — вторая точка пересечения окружности с прямой Тогда угол — вписанный и опирающийся на диаметр так что то есть — высота треугольника Отсюда

Ответ: 7,5 или 7,2.

Задание с5 № 484630

Найдите все значения параметра a, при каждом из которых система уравнений 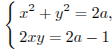имеет ровно два решения.

Решение.

Заменим первое уравнение разностью, а второе — суммой исходных уравнений:

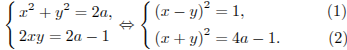
При второе уравнение системы, а, значит, и вся система решений не имеет. При получаем:

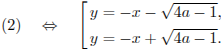
Ясно (см. рисунок), что при система имеет четыре решения (координаты точек A, B, C и D), а при  — два решения (координаты точек M и N).

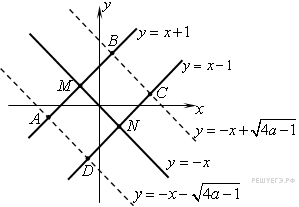
Ответ: .

Задание с6 № 500412

В ряд выписаны числа: , , …, , . Между ними произвольным образом расставляют знаки «+» и «−» и находят получившуюся сумму. Может ли такая сумма равняться: а) 12, если ? б) 0, если ? в) 0, если ? г) 5, если ?

Решение.

а) При следующей расстановке знаков получается требуемая сумма: . б) Среди выписанных 50 чисел 25 чётных и 25 нечётных. Поэтому любая сумма, которую можно получить, будет нечётной и не может равняться 0. в) Заметим, что . Значит, между 8 квадратами последовательных натуральных чисел можно расставить знаки так, что полученная сумма будет равняться 0:

При можно разбить все данные числа на группы по 8 чисел в каждой так, что сумма чисел в каждой группе равна 0, а значит, и сумма всех чисел равна 0. г) Как и в предыдущем пункте, расставим знаки между 88 числами , , ..., , таким образом, чтобы их сумма равнялась 0. Перед поставим знак «+». При такой расстановке знаков сумма равна Ответ: а) да; б) нет; в) да; г) да.

Конец формы