Вариант № 1940591

№ п/п	Номер	Тип	Правильный ответ
1	77347	B1	112
2	28763	B2	3
3	27709	B3	10
4	40319	B4	10620
5	315120	B5	2
6	27412	B6	8
7	26787	B7	7
8	27492	B8	-7
9	901	B9	9
10	285927	B10	0,6
11	27058	B11	12
12	27983	B12	180000
13	26597	B13	10
14	77489	B14	-6

↑ Задание 1 № 77347 тип B1В школе 800 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается? Решение. Учеников начальной школы 800   0,3 = 240, а учеников средней и старшей школы — 800 − 240 = 560. Значит, немецкий язык в школе изучают 560   0,2 = 112 учеников.

Ответ: 112.

↑ Задание 2 № 28763 тип B2

На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, сколько раз количество посетителей сайта РИА Новости принимало наибольшее значение.

Решение. Из диаграммы видно, что посетителей сайта РИА Новости принимало наибольшее значение 3 раза (см. рисунок).

Ответ: 3.

↑ Задание 3 № 27709 тип B3

Две стороны прямоугольника равны 6 и 8. Найдите длину разности векторов  и . Решение. Разность векторов и равна вектору . Вектор образует в прямоугольнике два прямоугольных треугольника. Поэтому по теореме Пифагора .

Ответ: 10.

↑ Задание 4 № 40319 тип B4

Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 4 кубометра пеноблоков и 2 мешка цемента. Для бетонного фундамента необходимо 4 тонны щебня и 40 мешков цемента. Кубометр пеноблоков стоит 2550 рублей, щебень стоит 580 рублей за тонну, а мешок цемента стоит 210 рублей. Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант?

Решение. Рассмотрим все варианты. Стоимость фундамента из пеноблоков складывается из стоимости пеноблоков 4   2550 = 10 200 руб., а также стоимости цемента 2   210 = 420 руб. Всего 420 + 10 200 = 10 620 руб. Стоимость бетонного фундамента складывается из стоимости цемента 40   210 = 8400 руб., а также стоимости щебня 4   580 = 2320 руб. Всего 8400 + 2320 = 10 720 руб. Первый вариант дешевле второго.

Ответ: 10 620.

↑ Задание 5 № 315120 тип B5

Найдите корень уравнения . Решение. Используем формулу :

Приведем другое решение:

Ответ:2.

↑ Задание 6 № 27412 тип B6

В треугольнике угол равен 90°, косинус внешнего угла при вершине равен –0,5, . Найдите . Решение. так как

Ответ: 8.

↑ Задание 7 № 26787 тип B7

Найдите , если . Решение. Выполним преобразования:

.

Ответ: 7.

З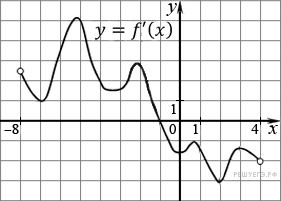 адание 8 № 27492 тип B8 (решено неверно или не решено)

На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наименьшее значение? Решение. На заданном отрезке производная функции положительна, поэтому функция на этом отрезке возрастает. Поэтому наименьшее значение функции достигается на левой границе отрезка, т. е. в точке .

Ответ: −7.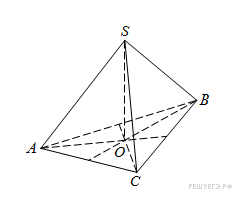

↑ Задание 9 № 901 тип B9

В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна 2; объем пирамиды равен 6. Найдите длину отрезка . Решение. отрезок высотой треугольной пирамиды , ее объем выражается формулой

Таким образом, Ответ: 9.

↑ Задание 10 № 285927 тип B10 В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам. Решение. Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна

Ответ: 0,6.

↑ Задание 11 № 27058 тип B11 Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на . Решение. Площадь боковой поверхности цилиндра   , поэтому

Ответ: 12.

↑ Задание 12 № 27983 тип B12

При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где м – длина покоящейся ракеты, км/с – скорость света, а – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с. Решение. Найдем, при какой скорости длина ракеты станет равна 5 м. Задача сводится к решению уравнения при заданном значении длины покоящейся ракеты м и известной величине скорости света км/с:

км/с.

Если скорость будет превосходить найденную, то длина ракеты будет менее 8 метров, поэтому минимальная необходимая скорость равна км/с.

Ответ: 180 000.

↑ Задание 13 № 26597 тип B13

Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба? Решение. Обозначим — количество литров воды, пропускаемой первой трубой в минуту, тогда вторая труба пропускает литров воды в минуту. Резервуар объемом 110 литров первая труба заполняет на 1 минуту дольше, чем вторая труба, отсюда имеем:

Таким образом, первая труба пропускает 10 литров воды в минуту. Ответ: 10.

↑ Задание 14 № 77489 тип B14

Найдите точку максимума функции . Решение. Заметим, что . Область определения функции — открытый луч . Найдем производную заданной функции:

Найдем нули производной:

Найденная точка лежит на луче . Определим знаки производной функции и изобразим на рисунке поведение функции:

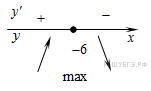
Искомая точка максимума .

Ответ: −6.

Начало формы