Проверка части с
Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь указанными критериями.
Начало формы
Задание с1 № 500427
а)
Решите уравнение
.
б) Найдите все корни этого уравнения,
принадлежащие отрезку
.
Решение.
а)
Запишем уравнение в виде:
Значит, или
,
откуда
,
,
или
,
откуда
,
.
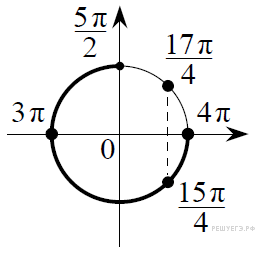
б) С помощью числовой окружности
отберём корни, принадлежащие отрезку
Получим
числа:
Ответ:
а)
,
;
,
;
б)
.
Задание с2 № 484571
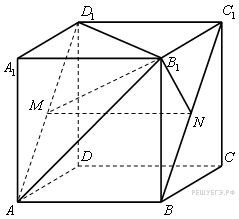
Дан
куб
.
Длина ребра куба равна 1. Найдите
расстояние от середины отрезка
до
плоскости
.
Решение.
М —
середина
,
N —
середина
.
Проведем перпендикуляр NH
из точки N
к плоскости
,
.
Значит,
.
Поэтому точка Н
лежит на отрезке
,
перпендикулярном
.
Искомый
отрезок NH
является высотой прямоугольного
треугольника
с
прямым углом N.
Поэтому
.
Ответ:
.
Задание с3 № 500388
Решите систему неравенств
Решение.
1. Решим первое неравенство системы. Сделаем замену .
Тогда
,
откуда находим решение первого неравенства
системы
.
2. Решим второе неравенство
системы:
.
Рассмотрим
два случая.
Первый случай:
.
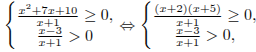
откуда
находим:
.
Все полученные значения переменной
удовлетворяют условию
.
Второй случай:
.
Учитывая
условие
,
получаем:
.
Решение второго неравенства исходной
системы:
3.
Поскольку
получаем
решение исходной системы неравенств:
Ответ:
Задание с4 № 484610
В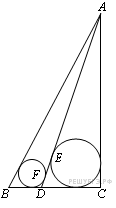
треугольнике ABC
,
,
.
Точка D
лежит на прямой BC
причем
.
Окружности, вписанные в каждый из
треугольников ADC
и ADB
касаются стороны AD
в точках E
и F.
Найдите длину отрезка EF.
Решение.
Пусть
,
,
.
Тогда
.
Возможны
два случая:
1. Точка D
лежит на отрезке BC.
Тогда
.
2.
Точка D
лежит вне отрезка BC.
Тогда
.
Ответ:
или
.
Задание с5 № 484633
При
каких значениях параметров а
и b
система
имеет
бесконечно много решений?
Решение.
На
координатной плоскости хОу
множество точек
,
удовлетворяющих любому из уравнений
системы — прямые. А тогда решением
системы будут точки пересечения этих
прямых. Поэтому исходная система будет
иметь бесконечное множество решений в
том и только в том случае, когда эти
прямые совпадают. В общем случае две
прямые, заданные уравнениями
и
совпадают,
если,
и
(при
они
имеют одну точку пересечения, при
и
точек
пересечения у них нет). Следовательно,
система будет иметь бесконечно много
решений в том случае, когда совместна
система
,
где
и
.
Решая систему, получаем
,
.
Ответ:
,
.
Задание с6 № 485960
В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2076. а) может ли в последовательности быть три члена? б) может ли в последовательности быть четыре члена? в) может ли в последовательности быть меньше 2076 членов?
Решение.
а) Нет, поскольку не делится на 2, а не является квадратом натурального числа. б) Последовательность не может быть арифметической прогрессией, поскольку не делится на 3. Последовательность не может быть геометрической прогрессией, поскольку не является кубом натурального числа. Если первые три члена образуют геометрическую прогрессию, а последние три – арифметическую, то эти числа: но уравнение не имеет целых корней. Если первые три члена образуют арифметическую прогрессию, а последние три – геометрическую, то эти числа: и где — натуральное число. Тогда последнее число должно равняться
но это не натуральное число. в) Да, например,