Результаты варианта 4 и 12

№ п/п	Номер	Тип	Правильный ответ
1	77365	B1	190
2	28764	B2	12
3	245007	B3	4,5
4	500633	B4	34
5	77374	B5	-2
6	27429	B6	8
7	77410	B7	42
8	119974	B8	7
9	245371	B9	5
10	285925	B10	0,36
11	27180	B11	7
12	28006	B12	60
13	26597	B13	10
14	77425	B14	-2

↑Задание 1 № 77365 тип B1

Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 200 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу? Решение. Скидка на покупку составит 200   0,05 = 10 рублей. Значит, держатель дисконтной карты заплатит за книгу 200 − 10 = 190 рублей.

Ответ: 190.

↑Задание 2 № 28764 тип B2

На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, какого числа количество посетителей сайта РИА Новости впервые приняло наибольшее значение.

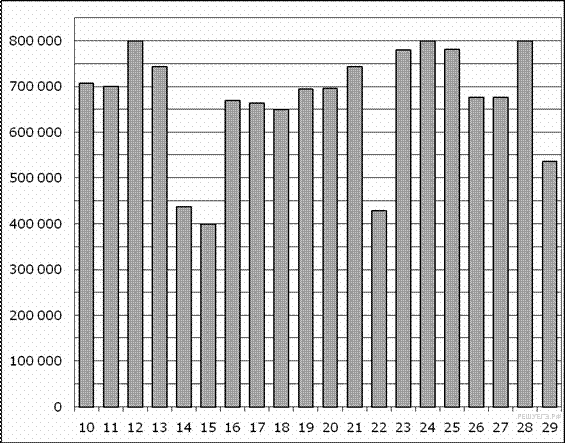Решение. Из графика видно, что 12 числа количество посетителей сайта РИА Новости было наибольшим за указанный период (см. рисунок). Ответ: 12.

Задание 3 № 245007 тип B3

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Решение. Площадь четырёхугольника равна разности площади большого квадрата, маленького прямоугольника и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому

см².

Правильный ответ: 4,5

↑Задание 4 № 500633 тип B4

Независимая экспертная лаборатория определяет рейтинги бытовых приборов R на основе средней цены P, а также оценок функциональности F, качества Q и дизайна D. Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

.

В таблице даны оценки каждого показателя для нескольких моделей электрических мясорубок. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

Модель мясорубки	Средняя цена	Функциональность	Качество	Дизайн
А	4800	4	1	4
Б	3700	2	2	2
В	3800	4	4	2
Г	6000	4	1	3

Решение. Вычислим рейтинг каждой модели. Рейтинг модели «А»: R_A = 4 (2 4 + 2 1 + 4) − 0,01 4800 = 8. Рейтинг модели «Б»: R_Б = 4 (2 2 + 2 2 + 2) − 0,01 3700 = 3. Рейтинг модели «В»: R_В = 4 (2 4 + 2 4 + 2) − 0,01 3800 = 34. Рейтинг модели «Г»: R_Г = 4 (2 4 + 2 1 + 3) − 0,01 6000 = −8. Наибольший рейтинг, равный 34, имеет модель «В». Правильный ответ: 34

↑Задание 5 № 77374 тип B5 Решите уравнение . Решение. Возведем в квадрат:

Ответ:  −2.

↑Задание 6 № 27429 тип B6

В треугольнике , косинус внешнего угла при вершине равен –0,5. Найдите . Решение.

.

Ответ: 8.

↑Задание 7 № 77410 тип B7 Найдите значение выражения . Решение. Выполним преобразования: .

Ответ: 42.

↑Задание 8 № 119974 тип B8

Прямая является касательной к графику функции . Найдите . Решение. Условие касания графика функции и прямой задаётся системой требований:

В нашем случае имеем:

О твет: 7.

↑Задание 9 № 245371 тип B9

Н айдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. Рассмотрим прямоугольный треугольник По теореме Пифагора

Ответ: 5.

↑Задание 10 № 285925 тип B10

П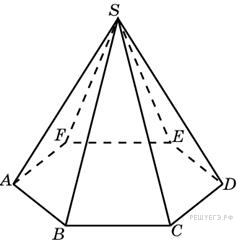 еред началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Решение. В первом туре Руслан Орлов может сыграть с 26 − 1 = 25 бадминтонистами, из которых 9 — из России. Значит вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна

Ответ: 0,36.

↑Задание 11 № 27180 тип B11

Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

Решение. Площадь основания равна .Из формулы для объема пирамиды найдем высоту:

.

В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем боковое ребро пирамиды по теореме Пифагора:

. Ответ: 7.

↑Задание 12 № 28006 тип B12

Трактор тащит сани с силой кН, направленной под острым углом к горизонту. Работа трактора (в килоджоулях) на участке длиной м вычисляется по формуле . При каком максимальном угле (в градусах) совершeнная работа будет не менее 2000 кДж? Решение. Задача сводится к решению неравенства на интервале при заданных значениях силы кН и длины пути м:

.

Ответ: 60.

Задание 13 № 26597 тип B13

Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба? Решение. Обозначим — количество литров воды, пропускаемой первой трубой в минуту, тогда вторая труба пропускает литров воды в минуту. Резервуар объемом 110 литров первая труба заполняет на 1 минуту дольше, чем вторая труба, отсюда имеем:

Таким образом, первая труба пропускает 10 литров воды в минуту.

Ответ: 10.

↑Задание 14 № 77425 тип B14 Найдите наименьшее значение функции на отрезке . Решение. Найдем производную заданной функции: .

Производная обращается в нуль в точках 0 и 2, заданному отрезку принадлежит число 2. Определим знаки производной функции и изобразим на рисунке поведение функции:

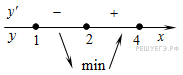
В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение: . Ответ: −2.

Начало формы

Задание С1 № 484546 Решите уравнение .

Решение.

Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а другой при этом не теряет смысла. Поэтому данное уравнение равносильно совокупности:

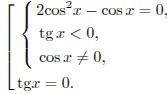
Из уравнения получаем либо (что противоречит условию ). Решением уравнения соответствуют две точки единичной окружности, одна из которых лежит в первой четверти (и значит, для нее неравенство не выполняется), а другая — в четвертой четверти (для нее неравенство выполняется, и решение уравнения дается формулой ). Теперь осталось выписать решение простейшего тригонометрического уравнения , т. е. , и записать ответ. Ответ: ; .

Вопрос: Не понимаю, почему cosx не может быть равно нулю.

Ответ: Так как tg(x)=sin(x)/cos(x), следовательно, cox(x) не может быть равен 0.

    

Задание С2 № 500816

Сторона основания правильной треугольной призмы равна 2, а диагональ боковой грани равна Найдите угол между плоскостью и плоскостью основания призмы.

Решение.

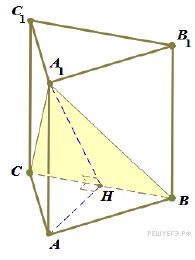Обозначим середину ребра (см. рис.). Так как треугольник равносторонний, а треугольник — равнобедренный, отрезки и перпендикулярны Следовательно, — линейный угол двугранного угла с гранями и Из треугольника найдем Из треугольника найдем Из треугольника найдем: Искомый угол равен

Ответ:

Задание С3 № 484580

Решите неравенство .

Решение. Пусть , тогда неравенство принимает вид:

.

Очевидно поэтому т. е. . Получаем:

.

Тогда

Ответ: , .

Задание С4 № 500470

Боковые стороны и трапеции равны 8 и 17 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 17,5. Прямые и пересекаются в точке . Найдите радиус окружности, вписанной в треугольник .

Решение.

В любой трапеции отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований трапеции, а средняя линия — полусумме оснований трапеции. В нашем случае полуразность оснований равна 7,5, а полусумма оснований равна 17,5, поэтому основания трапеции равны 10 и 25. Предположим, что , (рис. 1). Стороны и треугольников и параллельны, поэтому эти треугольники подобны с коэффициентом . Значит,

.

Заметим, что , поэтому треугольник прямоугольный с гипотенузой . Радиус его вписанной окружности равен:

.

Пусть теперь , (рис. 2). Аналогично предыдущему случаю можно показать, что радиус вписанной окружности треугольника равен 5. Треугольники и подобны с коэффициентом . Значит, радиус вписанной окружности треугольника равен . Ответ: 2; 5.

Задание С5 № 500196

Найдите все значения а, при каждом из которых неравенство выполняется для всех .

Решение.

Рассмотрим функцию . Эта функция возрастает на промежутке и убывает па промежутке . Исходное неравенство имеет вид , значит, график функции на отрезке должен находиться в пределах горизонтальной полосы: Отрезок не должен лежать на участке монотонности функции , иначе приращение на отрезке длины 5 будет не меньше 25, поэтому её график не поместится в полосе ширины 20. Следовательно, , откуда . Наибольшее значение функции на отрезке достигается либо при , либо при . Наименьшее значение функции на отрезке достигается при . Получаем систему:

,

откуда . Ответ:

Задание С6 № 484661

Перед каждым из чисел 3, 4, 5, . . . 11 и 14, 15, . . . 18 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 45 полученных результатов складывают. Какую наименьшую по модулю сумму и какую наибольшую сумму можно получить в итоге?

Решение.

1. Если все числа обоих наборов взяты с плюсами, то сумма максимальна и равна

.

2. Так как сумма нечетная, число нечетных слагаемых в ней нечетно, причем это свойство суммы не меняется при изменении знака любого ее слагаемого. Поэтому любая из получены сумм будет не четной, а значит, не будет равна 0. 3. Значение 1 сумма принимает, например, при следующей расстановке знаков у чисел:

.

Ответ: 1 и 1035.

Вариант № 1940274Конец формы

№ п/п	Номер	Тип	Правильный ответ
1	77335	B1	9,2
2	26863	B2	72
3	27815	B3	56
4	77358	B4	467,5
5	500141	B5	125
6	27382	B6	-0,25
7	26843	B7	8
8	27496	B8	5
9	245383	B9	45
10	285926	B10	0,2
11	72007	B11	216
12	27960	B12	20
13	99588	B13	4
14	282861	B14	-1

↑ Задание 1 № 77335 тип B1

Маша отправила SMS-сообщения с новогодними поздравлениями своим 16 друзьям. Стоимость одного SMS-сообщения 1 рубль 30 копеек. Перед отправкой сообщения на счету у Маши было 30 рублей. Сколько рублей останется у Маши после отправки всех сообщений? Решение. За 16 SMS-сообщений Маша заплатила 16   1,3 = 20,8 рубля. Значит, после отправки всех сообщений у Маши осталось: 30 − 20,8 = 9,2 рубля.

Ответ: 9,2.

↑ Задание 2 № 26863 тип B2

На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н   м. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0,036n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н   м? Ответ дайте в километрах в час.

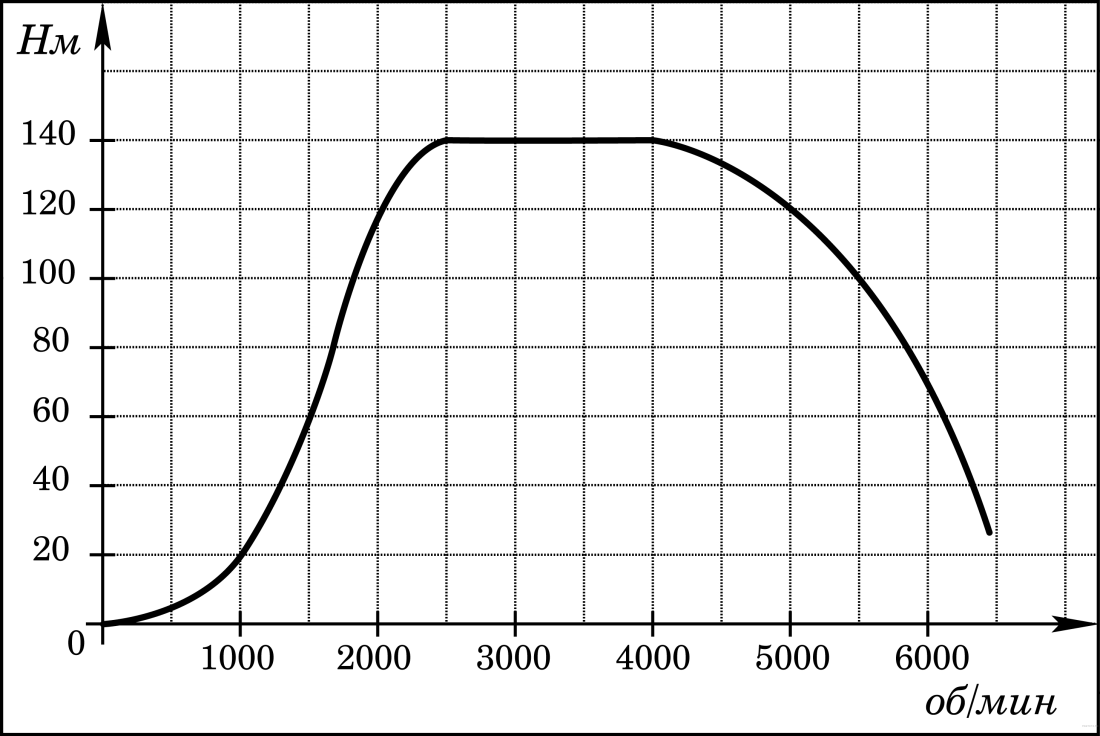
Решение. Для того, чтобы крутящий момент был не меньше 120 Н   м число оборотов двигателя в минуту n должно быть не меньше 2000 и не больше 5000 (см. график). Поэтому искомая наименьшая скорость определяется по формуле v = 0,036   2000 = 72 км/ч. Ответ: 72.

Вопрос: почему ответ в км/ч если по условию даны м/мин.

Ответ: В условии сказано, что при подстановке чисел в формулу скорость будет выражена в километрах в час.

↑ Задание 3 № 27815 тип B3

В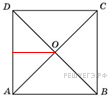 квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата. Решение. в квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно половине стороны квадрата, тогда

. Ответ: 56.

↑ Задание 4 № 77358 тип B4

В первом банке один фунт стерлингов можно купить за 47,4 рубля. Во втором банке 30 фунтов — за 1446 рублей. В третьем банке 12 фунтов стоят 561 рубль. Какую наименьшую сумму (в рублях) придется заплатить за 10 фунтов стерлингов? Решение. Рассмотрим все варианты. В первом банке 10 фунтов стерлингов будут стоить 47,4   10 = 474 руб. Во втором банке 10 фунтов стерлингов стоят 1446 : 3 = 482 руб. В третьем банке 1 фунт стерлингов стоит 561 : 12 = 187 : 4 = 46,75 руб. Значит, 10 фунтов стерлингов будут стоить 46,75   10 = 467,5 руб.

Ответ: 467,5.

Задание 5 № 500141 тип B5 Найдите корень уравнения Решение.Последовательно получаем: Ответ: 125.

↑ Задание 6 № 27382 тип B6

В треугольнике угол равен 90°, , . Найдите тангенс внешнего угла при вершине . Решение. так как

Ответ: –0,25.

↑ Задание 7 № 26843 тип B7 Найдите значение выражения . Решение. Выполним преобразования: . Ответ: 8.

↑ Задание 8 № 27496 тип B8

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

Решение. Точки экстремума соответствуют точкам смены знака производной — изображенным на графике нулем производной. Производная обращается в нуль в точках −6, −2, 2, 6, 9. На отрезке [−10; 10] функция имеет 5 точек экстремума. Ответ: 5.

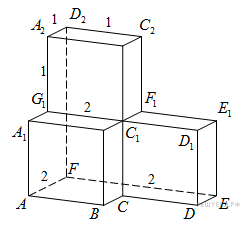
↑ Задание 9 № 245383 тип B9

Н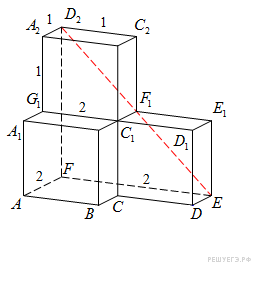 айдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Решение. – диагональ квадрата со стороной 2, значит, треугольник – прямоугольный и равнобедренный, угол равен . Ответ: 45.

↑ Задание 10 № 285926 тип B10

В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике. Решение. Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна

Ответ: 0,2.

↑ Задание 11 № 72007 тип B11

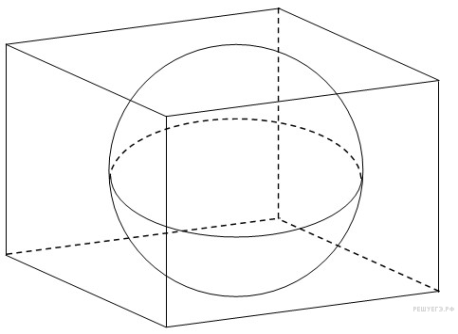В куб вписан шар радиуса 3. Найдите объем куба. Решение. Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем: . Ответ: 216.

↑ Задание 12 № 27960 тип B12

В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону , где – начальный уровень воды, м/мин², и м/мин постоянные, – время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах. Решение. Формулой, описывающей уменьшение высоты столба воды с течением времени является

.

Вода будет вытекать из бака, пока её начальный уровень не понизится до нуля. Определим требуемое на это время, решая уравнение :

Это означает, что по прошествии 20 минут вся вода вытечет из бака.

Ответ: 20.

↑ Задание 13 № 99588 тип B13

Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч? Решение. Пусть ч – время движения автомобилей до встречи. Первый автомобиль пройдет расстояние км, а второй –  км. Тогда имеем: .

Таким образом, автомобили встретятся через 4 часа.

Ответ: 4.

↑ Задание 14 № 282861 тип B14 Найдите наименьшее значение функции на отрезке . Решение. Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

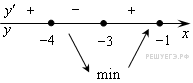
В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение: .

Ответ: −1.