Результаты варианта 12

В-1	В-2	В-3	В-4	В-5	В-6	В-7
8	70000	-6	4180	-1	8	-136

В-8	В-9	В-10	В-11	В-12	В-13	В-14
3	1	0,5	240	2	20	-2

Задание 1 № 26618 Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ? Решение.Во время распродажи шампунь станет стоить 160 − 0,25   160 = 120 рублей. Разделим 1000 на 120:

. Значит, можно будет купить 8 флаконов шампуня. Ответ: 8.

↑ Задание 2 № 28759 На диаграмме показано количество посетителей сайта РИА Новости в течение каждого часа 8 декабря 2009 года. По горизонтали указывается номер часа, по вертикали — количество посетителей сайта за данный час. Определите по диаграмме разность наибольшего и наименьшего количества посетителей за час в данный день.

Решение. Из диаграммы видно, что наибольшее и наименьшее количество посетителей составили 80 000 и 10 000 соответственно (см. рисунок). Их разность: 70 000 человек.

О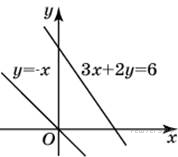 твет: 70 000.

↑ Задание 3 № 27690 Найдите ординату точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = −x. Решение. Решая совместно эти два уравнения, получаем, что x = 6, y = −6. Ответ: −6.

↑ Задание 4 № 26676

Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 500 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму в рублях заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?

Автомобиль	Топливо	Расход топлива (л на 100 км)	Арендная плата (руб. за 1 сутки)
А	Дизельное	7	3700
Б	Бензин	10	3200
В	Газ	14	3200

Цена дизельного топлива — 19 рублей за литр, бензина — 22 рублей за литр, газа — 14 рублей за литр. Решение. Рассмотрим все варианты. На 500 км автомобилю A понадобится 7   5 = 35 л дизельного топлива. Стоимость его аренды в сутки складывается из арендной платы 3700 руб. и затрат на дизельное топливо 35   19 = 665 руб. Всего 4365 руб. На 500 км автомобилю Б понадобится 10   5 = 50 л бензина. Стоимость его аренды в сутки складывается из арендной платы 3200 руб. и затрат на бензин 50   22 = 1100 руб. Всего 4300 руб. На 500 км автомобилю В понадобится 14   5 = 70 л газа. Стоимость его аренды в сутки складывается из арендной платы 3200 руб. и затрат на газ 70   14 = 980 руб. Всего 4180 руб. Стоимость самого дешевого заказа составляет 4180 рублей. Ответ: 4180.

↑ Задание 5 № 26650 Найдите корень уравнения . Решение. Перейдем к одному основанию степени:

Ответ: −1.

↑ Задание 6 № 27286 В треугольнике , . Найдите . Решение. Треугольник равнобедренный, значит, высота делит основание пополам.

. Ответ: 8.

↑ Задание 7 № 77390 Найдите значение выражения . Решение. Выполним преобразования:

. Ответ: -136.

↑ Задание 8 № 500248 На рисунке изображён график дифференцируемой функции . На оси абсцисс отмечены девять точек: . Среди этих точек найдите все точки, в которых производная функции отрицательна. В ответе укажите количество найденных точек.

Решение. Производная функции отрицательна на тех интервалах, на которых функция убывает. Если сторону клетки принять за единицу, то функция убывает на интервалах (−4,4; −0,7) и (2,6;+∞). В них содержатся целые точки x₄, x₅, x₉. Их 3 штуки. Ответ: 3.

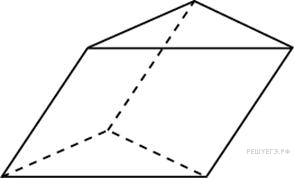
↑ Задание 9 № 284353 В правильной треугольной пирамиде точка  — середина ребра ,  — вершина. Известно, что , а площадь боковой поверхности равна 3. Найдите длину отрезка . Решение. Площадь боковой поверхности правильной пирамиды равна произведению апофемы на полупериметр основания. Поэтому

Ответ: 1.

↑ Задание 10 № 320178 На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной? Решение. На клавиатуре телефона 10 цифр, из них 5 четных: 0, 2, 4, 6, 8. Поэтому вероятность того, что случайно будет нажата четная цифра равна 5 : 10 = 0,5. Ответ: 0,5.

↑ Задание 11 № 27150 В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы. Решение. Для вычисления боковой поверхности призмы воспользуемся формулой , где – длина бокового ребра, а – площадь перпендикулярного сечения призмы:

. Ответ: 240.

↑ Задание 12 № 27962 Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением , где – время в минутах, К, К/мин , К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах. Решение. Найдем, в какой момент времени после начала работы температура станет равной К. Задача сводится к решению уравнения при заданных значениях параметров a и b:

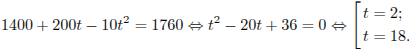Через 2 минуты после включения прибор нагреется до 1760 К, и при дальнейшем нагревании может испортиться. Таким образом, прибор нужно выключить через 2 минуты. Ответ: 2.

↑ Задание 13 № 99596 Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? Решение. Пусть км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна км/ч. Пусть первый раз мотоциклисты поравняются через часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому

. Таким образом, мотоциклисты поравняются через  часа или через 20 минут. Ответ: 20.

Приведём другое решение. Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.

↑ Задание 14 № 77499 Найдите наименьшее значение функции на отрезке . Решение. Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

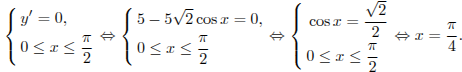
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

. Ответ: -2.

Начало формы

Задание С1 № 485940

Решите уравнение Укажите корни, принадлежащие отрезку

Решение. Сделаем замену и получим квадратное уравнение корнями которого являются числа и Уравнение не имеет решений, а из уравнения находим: или

.

Найдем корни, принадлежащие отрезку .

, .

Отрезку принадлежат только корни и  . Ответ: . Отрезку принадлежат корни: и .

Задание С2 № 485966

В правильной четырехугольной призме высота равна 1, а сторона основания равна . Точка  — середина ребра . Найдите расстояние от точки до плоскости .

Решение.

Рассмотрим треугольную пирамиду . Ее объем можно выразить двумя способами: 1) . 2) , где искомое расстояние. Приравняем выражения для объемов и выразим его:

Найдем площадь равнобедренного треугольника . Проведем в нем высоту .

.

.

.

.

.

Следовательно, искомое расстояние . Ответ: .

Задание С3 № 484601

Решите систему неравенств

Решение. По смыслу задачи , откуда . При этих значениях переменной: имеем:

.Тогда:

.

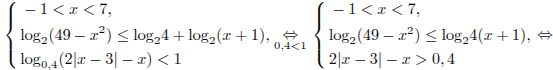
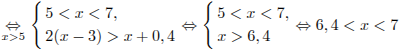Ответ:.

Задание С4 № 500369

В треугольнике известны стороны: . Окружность, проходящая через точки и , пересекает прямые и соответственно в точках и , отличных от вершин треугольника. Отрезок касается окружности, вписанной в треугольник . Найдите длину отрезка .

Решение.

Обе точки и не могут лежать вне треугольника, поскольку в этом случае отрезок не может касаться вписанной окружности. Значит, по крайней мере одна из этих точек лежит на стороне треугольника. Пусть обе точки и лежат на сторонах треугольника. Четырехугольник  — вписанный, следовательно,

Значит, треугольник подобен треугольнику , так как угол  — общий. Пусть коэффициент подобия равен , тогда , , . Суммы противоположных сторон описанного четырехугольника равны:

Подставляя известные значения сторон, находим . Следовательно, . Пусть точка лежит на продолжении стороны . Углы и равны, поскольку опираются на одну дугу. Значит, треугольник подобен треугольнику , так как угол  — общий. Более того, они описаны около одной и той же окружности. Следовательно, коэффициент подобия равен 1, то есть, треугольники и равны, поэтому . Заметим, что и точка действительно лежит на продолжении стороны . Если точка лежит на продолжении стороны , то , но, аналогично предыдущему случаю, получаем . Значит, этот случай не достигается. Ответ: .

Задание С5 № 484644

Найти все значения а, при каждом из которых функция имеет более двух точек экстремума.

Решение. 1. Функция f имеет вид а) при : , поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии ; б) при : , поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии . Все возможные виды графиков функции показаны на рисунках:

Графики обеих квадратичных функции проходят через точку . 3. Функция имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1):

.

Ответ: ; .

Задание С6 № 484666

Каждое из чисел 2, 3, ... , 7 умножают на каждое из чисел 13, 14, ... , 21 и перед каждым из полученных произведении произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Решение.

1. Если все произведения взяты со знаком плюс, то их сумма максимальна и равна

.

2. Так как сумма оказалась нечетной, то чисто нечетных слагаемых в ней нечетно, причем это свойство всей суммы не меняется при смене знака любого ее слагаемого. Поэтому любая из получающихся сумм будет нечетной, а значит, не будет равна 0. 3. Значение 1 сумма принимает, например, при такой расстановке знаков у произведений, которая получится при раскрытии следующих скобок:

.

Ответ: 1 и 4131.

Конец формы