Проверка части с
Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь указанными критериями.
Начало формы
Задание С1 № 484541
Решите
уравнение
.
Решение.
Найдем
ОДЗ:
.
Найдем корни числителя:
О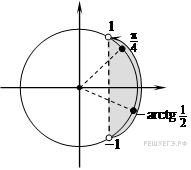
тметим
корни на тригонометрической окружности:
С
учетом ОДЗ (см. рис.) получаем:
Ответ:
.
Углы −1 и 1 радиан являются границами ОДЗ.
1 радиан примерно равен 57 градусам.
Задание С2 № 485992
Дана
правильная четырехугольная пирамида
Боковое
ребро
сторона
основания равна 2. Найдите расстояние
от точки
до
плоскости
где
—
середина ребра
Решение.
Построим
сечение ADMK,
где K
— середина ребра SB.
Покажем, что искомое расстояние равно
длине SQ,
где Q
— середина апофемы SN.
Действительно, пусть P
— середина стороны AD,
AD
перпендикулярна SP
и NP,
поэтому AD
перпендикулярна плоскости SNP,
а тогда и KM
— средняя линия боковой грани —
перпендикулярна PQ.
С другой стороны, SQ
перпендикулярна KM.
Тогда SQ
— перпендикуляр к плоскости сечения,
его длина равна искомому расстоянию.
Рассмотрим сечение NSP.
Имеем:
.
Значит, треугольник SNP равносторонний. Искомое расстояние равно SQ = 0,5SN = 1. Ответ: 1.
Задание С3 № 484605
Решите
систему неравенств
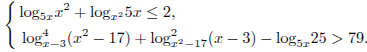
Решение.
Заметим,
что по смыслу задачи
,
а значит, оба слагаемых в левой части
первого неравенства положительны.
Поскольку слагаемые взаимно обратные,
их сумма не меньше двух. Тогда неравенство
выполнено в том и только в том случае,
когда оба слагаемых равны 1.
Имеем:
.
Осталось
проверить, является ли найденное решение
первого неравенства решением второго
неравенства. Выполним проверку:
.
Следовательно,
число 5 является решением системы
неравенств.
Ответ:
.
И неужели за такое вот решение проверяющие поставят 3 балла? А как же ОДЗ, в котором будет 8 случаев???
Решение верно. Поставят полный балл.
Задание С4 № 484612
В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону BC точками M и N так, что . Найдите BC если .
Решение.
Пусть E — точка пересечения биссектрис, BM=x, MN=y NC=z. Так как , то точка M лежит между точками B и N возможны 2 случая. 1. Точка E — внутри параллелограмма. Треугольники ABN и DMC равнобедренные, следовательно, , откуда, .
2. Точка E — вне параллелограмма. Тогда , откуда .
Ответ: 16 или 48.
Задание С5 № 484649
Найдите все положительные значения а, при каждом из которых система имеет единственное решение.
Решение.
Если , то уравнение задает окружность с центром в точке радиуса 2, а если , то оно задаёт окружность с центром в точке того же радиуса (см. рис.).
При положительных значениях параметра а уравнение задаст окружность с центром в точке радиуса а. Поэтому задача состоит в том, чтобы найти все значения параметра а, при каждом из которых окружность имеет единственную общую точку с объединением окружностей и . Из точки С проведём луч и обозначим и точки его пересечения с окружностью , где лежит между С и . Так как , то , .
При или окружности и не пересекаются. При окружности и имеют две общие точки. При или окружности и касаются. Из точки С проведём луч и обозначим и точки его пересечения с окружностью , где лежит между точками и . Так как , то
, .
При или окружности и не пересекаются. При окружности и имеют две общие точки. При или окружности и касаются. Исходная система имеет единственное решение тогда и только тогда, когда окружность касается ровно одной из двух окружностей и и не пересекается с другой. Так как , то условию задачи удовлетворяют только числа и . Ответ: 3; .
Задание С6 № 485960
В возрастающей последовательности натуральных чисел каждые три последовательных члена образуют либо арифметическую, либо геометрическую прогрессию. Первый член последовательности равен 1, а последний 2076. а) может ли в последовательности быть три члена? б) может ли в последовательности быть четыре члена? в) может ли в последовательности быть меньше 2076 членов?
Решение.
а) Нет, поскольку не делится на 2, а не является квадратом натурального числа. б) Последовательность не может быть арифметической прогрессией, поскольку не делится на 3. Последовательность не может быть геометрической прогрессией, поскольку не является кубом натурального числа. Если первые три члена образуют геометрическую прогрессию, а последние три – арифметическую, то эти числа: но уравнение не имеет целых корней. Если первые три члена образуют арифметическую прогрессию, а последние три – геометрическую, то эти числа: и где — натуральное число. Тогда последнее число должно равняться
но это не натуральное число. в) Да, например,