Задание с1 № 484542

Решите систему уравнений

Решение.

Из второго уравнения получаем:

или .

Если , то из первого уравнения . Уравнение не имеет решений. Если то , и из первого уравнения получаем: . Ответ: .

Вопрос:а можно написать в ответе:+-arccos1/25+2пn,-1/25.??

Антон Лобашов (Тихвин):

Ответ: Гость 06.06.2012 12:26:

Почему при y=-5/4 нет решений?

Ответ: При y=-5/4, cos(x)>1, чего не может быть.

Задание с2 № 485981

Основание прямой четырехугольной призмы — прямоугольник , в котором , . Найдите угол между плоскостью основания призмы и плоскостью, проходящей через середину ребра перпендикулярно прямой , если расстояние между прямыми и равно 13.

Решение.

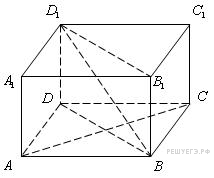Расстояние между прямыми и равно расстоянию между основаниями, то есть высоте призмы. Значит, высота призмы равна 13. Угол между плоскостями равен углу между прямыми, перпендикулярными этим плоскостям. Поэтому искомый угол равен углу между ребром и прямой . Рассмотрим треугольник . Его катеты равны Значит, Ответ: 45

Задание с3 № 484598

Решите систему неравенств

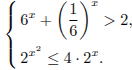
Решение.

Последовательно получаем:

Ответ: .

Задание с4 № 484615

Дан ромб ABCD с диагоналями и . Проведена окружность радиуса с центром в точке пересечения диагоналей ромба. Прямая, проходящая через вершину B касается этой окружности и пересекает прямую CD в точке M. Найдите CM.

Решение.

Пусть точка M лежит между C и D, P, — точка касания прямой BM с данной окружностью, O — центр ромба.

По теореме Пифагора . Обозначим

.

Из прямоугольных треугольников и находим, что

.

Применяя теорему синусов к треугольнику BMD получим, что , поэтому

.

Следовательно, . Пусть теперь точка лежит на продолжении стороны за точку Тогда по теореме о внешнем угле треугольника

.

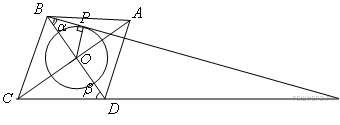
Далее, рассуждая аналогично, получим, что

.

Следовательно, . Ответ: или .

Задание с5 № 500965

Найдите все значения параметра при каждом из которых на интервале существует хотя бы одно число , не удовлетворяющее неравенству

Решение.

Преобразуем неравенство:

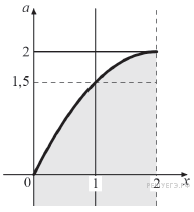Неравенство определяет на плоскости полосу, заключенную между прямыми и Неравенство задаёт часть плоскости, ограниченную сверху параболой. На рисунке видно, что на интервале есть , не удовлетворяющие неравенству, только если Ответ:

Задание с6 № 484655

Найдите все такие пары натуральных чисел a и b, что если к десятичной записи числа a приписать справа десятичную запись числа b, то получится число, большее произведения чисел a и b на 32.

Решение.

, где k — число цифр в числе b, . Тогда , иначе

.

Непосредственно проверяем . Соответственно: . Ответ: 12 и 8; 23 и 9.

Конец формы

Вариант № 1934413Вариант № 1934413Конец формы

Конец формы

Конец формы

Конец формы

Результаты Вариант № 14

Фамилия, имя__________________________________________

В-1	В-2	В-3	В-4	В-5	В-6	В-7
44	13400	10	32	10	4	0,25

В-8	В-9	В-10	В-11	В-12	В-13	В-14
7	60	0,978	110	100	45	-6

Задание 1 № 77334

В обменном пункте 1 гривна стоит 3 рубля 70 копеек. Отдыхающие обменяли рубли на гривны и купили 3 кг помидоров по цене 4 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа. Решение. За 3 кг помидоров отдыхающие заплатили 4   3 = 12 гривен. Значит, в рублях они заплатили: 12   3,7 = 44,4 рубля. Округляем до целого числа, получаем 44. Ответ: 44.

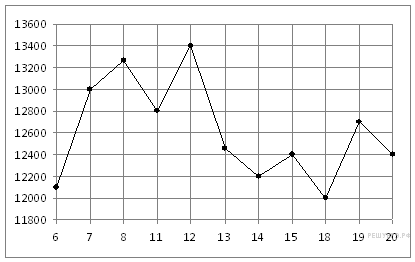
↑ Задание 2 № 26873

На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену никеля на момент закрытия торгов в указанный период (в долларах США за тонну).

Решение. Из графика видно, что наибольшая цена одной тонны никеля составляла 13 400 долларов США (см. рисунок). Ответ: 13 400.

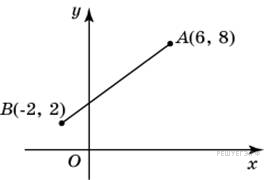
↑ Задание 3 № 27662 Найдите длину отрезка, соединяющего точки A(6; 8) и (−2; 2). Решение. Длина отрезка определяется следующим выражением:

Ответ: 10.

↑ Задание 4 № 316048 Независимая экспертная лаборатория определяет рейтинг бытовых приборов на основе коэффициента ценности, равного 0,01 средней цены , показателей функциональности , качества и дизайна . Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле

В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических мясорубок. Определите наивысший рейтинг представленных в таблице моделей электрических мясорубок.

Модель мясорубки	Средняя цена	Функциональность	Качество	Дизайн
А	4600	2	0	2
Б	5500	4	3	1
В	4800	4	4	4
Г	4700	2	1	4

Решение. Рассмотрим все варианты. Модель А:

Модель Б: Модель В: Модель Г: Тем самым, наивысший рейтинг имеет модель В, он равен 32. Ответ: 32.

↑ Задание 5 № 26652 Найдите корень уравнения .

Решение. Перейдем к одному основанию степени:

. Ответ: 10.

↑ Задание 6 № 27802 Найдите биссектрису треугольника , проведенную из вершины , если стороны квадратных клеток равны 1. Решение. по рисунку видно, что , значит, биссектриса, проведенная из вершины , также будет делить основание пополам. Построим отрезок . Видно, что он равен 4.

Ответ: 4.

↑ Задание 7 № 26837 Найдите значение выражения при . Решение. Выполним преобразования: . Ответ: 0,25.

↑ Задание 8 № 119979 Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с? Решение. Найдем закон изменения скорости: м/с. Чтобы найти, в какой момент времени скорость была равна 2 м/с, решим уравнение: 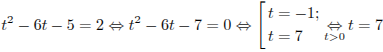Ответ: 7.

↑ Задание 9 № 245373

Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Решение. Рассмотрим треугольник где т. к. являются диагоналями в равных прямоугольниках. Следовательно, треугольник – равносторонний, поэтому все его углы равны Ответ: 60.

↑ Задание 10 № 320200

На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных. Решение. Пусть завод произвел тарелок. В продажу поступят все качественные тарелки и 20% невыявленных дефектных тарелок: тарелок. Поскольку качественных из них , вероятность купить качественную тарелку равна

О твет: 0,978.

↑ Задание 11 № 25601

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Решение. Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:

.

2∙(5∙5+3∙5+3∙5)=110 Ответ: 110.

↑ Задание 12 № 27987 Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной км с постоянным ускорением км/ч², вычисляется по формуле . Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 5000 км/ч². Ответ выразите в км/ч. Решение. Найдем, при какой скорости автомобиль приобретает ускорение 5000 км/ч². Задача сводится к решению уравнения при заданном значении расстояния км:

.

Если скорость будет превосходить найденную, то ускорение автомобиля более 5000 км/ч², поэтому минимальная необходимая скорость равна 100 км/ч. Ответ: 100.

↑ Задание 13 № 99593 Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч. Решение. Скорость товарного поезда меньше, чем скорого на 750 м/мин или на . Пусть км/ч — скорость товарного поезда, тогда скорость скорого поезда км/ч. На путь в 180 км товарный поезд тратит времени на 2 часа больше, чем скорый, отсюда имеем:

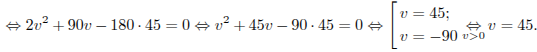Ответ: 45.

↑ Задание 14 № 315127 Найдите наименьшее значение функции на отрезке . Решение. Найдем производную заданной функции:

Найдем нули производной:

Отметим на рисунке нули производной и поведение функции на заданном отрезке: Следовательно, наименьшим значением функции на заданном отрезке является ее значение в точке минимума. Найдем его:

Ответ: −6.