Задание с6 № 500452

Каждое из чисел 1, −2, −3, 4, −5 , 7, −8, 9 по одному записывают на 8 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5 , 7, −8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?

Решение.

а) Среди восьми данных чисел нет противоположных. Значит, сумма чисел на каждой карточке не равна 0. Поэтому всё произведение не может равняться нулю. б) Среди восьми данных чисел пять нечётных. Значит, на какой-то карточке попадётся два нечётных числа, и их сумма чётная. Поэтому всё произведение чётно и не может равняться 1. в) Среди восьми данных чисел пять нечётных. Значит, хотя бы на двух карточках с обеих сторон написаны нечётные числа, и сумма чисел на каждой из этих карточек чётная. Поэтому всё произведение делится на 4. Наименьшее целое положительное число, делящееся на 4, это 4. Оно получается при следующем наборе пар чисел на карточках: (1;−2); (−2;1); (−3;4); (4;−3); (−5;7); (7;−5); (−8;9); (9;−8). Ответ: а) нет; б) нет; в) 4.

Вариант № 1939 447

Конец формы

№ п/п	Номер	Тип	Правильный ответ
1	318580	B1	186
2	263863	B2	1
3	27680	B3	6
4	319557	B4	-46
5	500141	B5	125
6	27282	B6	4
7	77406	B7	5
8	27499	B8	6
9	915	B9	15
10	500999	B10	0,4
11	27084	B11	4,5
12	319859	B12	35
13	99585	B13	22
14	26715	B14	20

↑ Задание 1 № 318580 тип B1

Рост Джона 6 футов 1 дюйм. Выразите рост Джона в сантиметрах, если 1 фут равен 0,305 м, а 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров. Решение. Рост Джона составляет 6   0,305   100 + 2,54 = 185,54 см. Округляя, получаем 186 см.

Ответ: 186.

↑ Задание 2 № 263863 тип B2

Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч? Решение. Из графика видно, что при скорости 200 км в час действующая на крылья подъемная сила равна одной тонне силы.

Ответ: 1.

↑ Задание 3 № 27680 тип B3

Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма. Найдите ординату точки . Решение. Пусть точка P является серединой отрезков OA и BC. Координаты точки P вычисляются следующим образом:

, ,

но с другой стороны, , .

Поэтому , .

Ответ: 6.

↑ Задание 4 № 319557 тип B4

Рейтинговое агентство определяет рейтинг соотношения «цена-качество» электрических фенов для волос. Рейтинг вычисляется на основе средней цены и оценок функциональности , качества и дизайна . Каждый отдельный показатель оценивается экспертами по пятибалльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

В таблице даны оценки каждого показателя для нескольких моделей фенов. Определите, какая модель имеет наименьший рейтинг. В ответ запишите значение этого рейтинга.

Модель фена	Средняя цена	Функциональность	Качество	Дизайн
А	1200	1	3	1
Б	3200	2	3	4
В	5500	3	0	0
Г	5700	3	2	3

Решение. Рассмотрим все варианты. Модель А: Модель Б: Модель В: Модель Г: Таким образом, наименьший рейтинг имеет модель В. Он равен −46. Ответ: −46.

↑ Задание 5 № 500141 тип B5 Найдите корень уравнения Решение. Последовательно получаем:

Ответ: 125.

↑ Задание 6 № 27282 тип B6 (решено неверно или не решено)

В треугольнике угол равен 90°, – высота, , . Найдите . Решение.

.

Ответ: 4.

↑ Задание 7 № 77406 тип B7 Найдите значение выражения . Решение. Выполним преобразования:

.

Ответ: 5.

↑ Задание 8 № 27499 тип B8

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Решение. Промежутки возрастания функции f(x) соответствуют промежуткам, на которых производная функции положительна, то есть интервалам (−11; −10), (−7; −1), (2; 3). Наибольший из них — интервал (−7; −1), длина которого 6.

Ответ: 6.

↑ Задание 9 № 915 тип B9

В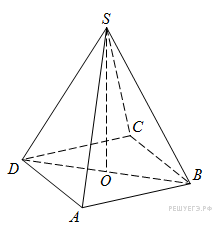 правильной четырехугольной пирамиде точка – центр основания, – вершина, =12, =18. Найдите боковое ребро Решение. в правильной пирамиде вершина проецируется в центр основания, следовательно является высотой пирамиды. тогда по теореме Пифагора

Ответ: 15.

↑ Задание 10 № 500999 тип B10

В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане. Решение. Двухрублевые монеты могут лежать в одном кармане, если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий:

Ответ: 0,4.

Приведем другое решение. Количество способов взять 3 монеты из 6, чтобы переложить их в другой карман, равно Количество способов выбрать 3 рублевых монеты из 4 рублевых монет равно 4. Количество способов взять вместе с двумя двухрублевыми монетами одну рублевую монету из имеющихся 4 рублевых монет тоже равно 4. Поэтому искомая вероятность того, что двухрублевые монеты лежат в разных карманах, равна

Правильный ответ: 0,4

↑ Задание 11 № 27084 тип B11

Н айдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны . Решение. Объем прямой призмы равен , где — площадь основания, а — боковое ребро. Площадь правильного шестиугольника со стороной , лежащего в основании, задается формулой

.

Тогда объем призмы равен . Ответ: 4,5.

↑ Задание 12 № 319859 тип B12 Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности , оперативности , объективности публикаций , а также качества сайта . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.

Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид

Каким должно быть число , чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1? Решение. Поскольку показатели максимальны, они равны 5. Подставим значения в формулу:

Ответ:35.

↑ Задание 13 № 99585 тип B13

Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней. Решение. В первый день Вера подписала открыток, во второй – , …, в последний – открыток. Всего было подписано открыток. Количество подписываемых открыток увеличивалось на каждый день.

.

Тогда за четвертый день было подписано

открыток.

Ответ: 22.

↑ Задание 14 № 26715 тип B14

Найдите наибольшее значение функции на отрезке . Решение. Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:

В точке заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

.Ответ: 20.

Начало формы