Задание с1 № 500638 а) Решите уравнение . Б) Найдите все корни этого уравнения, принадлежащие промежутку .
Решение.а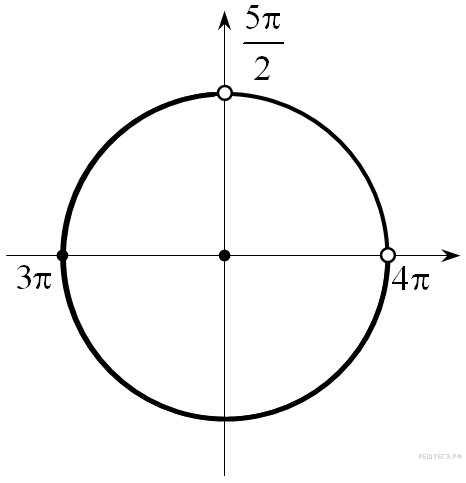
)
Решим уравнение:
б) Отбор корней. Составим двойное неравенство:
Тогда
искомый корень
.
Ответ: а)
;
б)
.
Задание с2 № 500387
На ребре куба отмечена точка так, что . Найдите угол между прямыми и .
Решение.
Примем ребро куба за единицу. Тогда . Поскольку , получаем: и . Проведем через точку прямую, параллельную . Она пересекает ребро в точке , причем треугольники и равны. Искомый угол равен углу (или смежному с ним). В прямоугольном треугольнике с прямым углом
В прямоугольном треугольнике с прямым углом
В треугольнике
откуда
, тогда
Ответ может быть представлен и в другом виде: или Ответ: .
Задание с3 № 500449
Решите
систему неравенств
Решение.
1.
Решим первое неравенство системы.
Сделаем замену
.
.
Тогда
,
откуда находим решение первого неравенства
системы:
.
2. Решим второе неравенство системы.
Рассмотрим два случая.
Первый
случай:
.
.
Учитывая
условие
,
получаем:
.
Второй случай:
.
.
Учитывая
условие
,
получаем:
;
.
Решение второго неравенства
системы:
.
3. Решение исходной системы неравенств:
.
Ответ:
;
;
.
Задание с4 № 500349
Дан треугольник со сторонами 115, 115 и 184. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Решение.
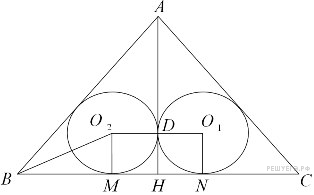Рассмотрим
равнобедренный треугольник
,
в котором
,
Пусть
—
высота треугольника
.
Тогда
—
середина
.
Обозначим
Тогда
,
,
Предположим,
что окружность радиуса
с
центром
вписана
в угол
и
касается основания
в
точке
,
а окружность того же радиуса с центром
вписана
в угол
,
касается основания
в
точке
,
а первой окружности — в точке
.
Центр окружности, вписанной в угол,
лежит на его биссектрисе, поэтому
,
а
Из
прямоугольного треугольника
находим:
.
Тогда
.
Линия
центров касающихся окружностей проходит
через точку их касания, поэтому
,
значит,
,
поскольку
—
прямоугольник. Следовательно,
,
откуда находим
.
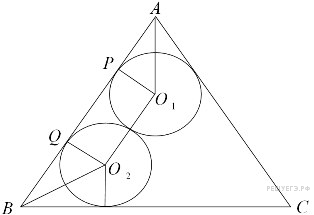Пусть
теперь окружность радиуса
с
центром
вписана
в угол
и
касается боковой стороны
в
точке
,
вторая окружность радиуса
с
центром
вписана
в угол
,
касается боковой стороны
в
точке
,
а также касается первой окружности.
Из прямоугольных треугольников
и
находим:
,
.
Следовательно,
,
откуда
находим
.
В случае, когда окружности вписаны
в углы
и
,
получим тот же результат.
Ответ:
23 или 20.
Задание с5 № 484648
Найдите
все значения параметра а,
при каждом из которых система
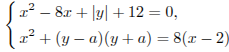имеет
ровно 8 решений.
Решение.
Преобразуем систему:
Первое уравнение задает части двух парабол:
(см. рисунок).
Второе
уравнение задает окружность радиусом
с
центром
.
На рисунке видно, что система имеет
восемь решений, только если радиус
окружности меньше 2 и окружность дважды
пересекает каждую ветвь каждой из
парабол. Это условие в силу симметрии
равносильно тому, что окружность
пересекает правую ветвь параболы
в
двух точках с положительными ординатами.
Получаем уравнение
,
откуда
,
которое должно иметь два различных положительных корня. Следовательно, дискриминант и свободный член этого уравнения должны быть положительны:
откуда
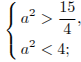
Ответ:
,
.