Задание с5 № 484645

Найдите все значения параметра а, при каждом из которых система имеет единственное решение.

Решение.

Преобразуем исходную систему:

Уравнение задает пару пересекающихся прямых и . Система

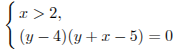
задает части этих прямых, расположенные правее прямой , т. е. лучи DB и CE (без точек B и С), см. рис.

Уравнение задает прямую m с угловым коэффициентом a, проходящую через точку . Следует найти все значения а, при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и СЕ. а) Прямая АB задается уравнением . Поэтому при прямая m не пересечет ни луч BD, ни луч СЕ. б) Прямая АС задается уравнением . Поэтому при прямая m пересечет луч BD, но не пересечет луч СЕ. в) При прямая m пресечет и луч BD, и луч СЕ. г) Наконец, при прямая m пересечет только луч СЕ, а при она не пересечет ни луч BD, ни луч СЕ. Ответ: , .

Задание с6 № 484666

Каждое из чисел 2, 3, ... , 7 умножают на каждое из чисел 13, 14, ... , 21 и перед каждым из полученных произведении произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Решение.

1. Если все произведения взяты со знаком плюс, то их сумма максимальна и равна

.

2. Так как сумма оказалась нечетной, то чисто нечетных слагаемых в ней нечетно, причем это свойство всей суммы не меняется при смене знака любого ее слагаемого. Поэтому любая из получающихся сумм будет нечетной, а значит, не будет равна 0. 3. Значение 1 сумма принимает, например, при такой расстановке знаков у произведений, которая получится при раскрытии следующих скобок:

.

Ответ: 1 и 4131.

Результаты Вариант № 413

№ п/п	Номер	Тип	Правильный ответ
1	77337	B1	7
2	26866	B2	3
3	27730	B3	20
4	500636	B4	21
5	77368	B5	-1,5
6	27397	B6	0,25
7	26747	B7	2
8	500035	B8	2
9	318474	B9	0,6
10	320187	B10	5
11	27175	B11	0,25
12	28000	B12	50
13	99606	B13	70
14	26713	B14	-15

↑ Задание 1 № 77337 тип B1

В школе есть трехместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 20 человек? Решение. Разделим 20 на 3: . Значит, в поход нужно взять 7 палаток. Ответ: 7.

↑ Задание 2 № 26866 тип B2

На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 60 °C до температуры 90 °C.

Решение. Из графика видно, что двигатель нагревался от температуры 60 °C до температуры 90 °C с 5-й по 8-ю минуту, таким образом, он нагревался 3 минуты.

О твет: 3.

↑ Задание 3 № 27730 тип B3 Найдите сумму координат вектора  + . Решение. Координаты суммы векторов равны сумме соответствующих координат. Тогда вектор имеет координаты . Поэтому сумма координат вектора равна .

Ответ: 20.

↑ Задание 4 № 500636 тип B4

Рейтинговое агенство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг начисляется на основе средней цены Pи оценок функциональности F, качества Q и дизайна D. Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

.

В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

Модель печи	Средняя цена	Функциональность	Качество	Дизайн
А	5800	2	2	4
Б	4200	1	0	1
В	4300	4	3	2
Г	3900	2	0	3

Решение. Вычислим рейтинг каждой модели. Рейтинг модели «А»: R_A = 8 (2 + 2) + 4 4 − 0,01 5800 = −10. Рейтинг модели «Б»: R_Б = 8 (1 + 0) + 4 1 − 0,01 4200 = −30. Рейтинг модели «В»: R_В = 8 (4 + 3) + 4 2 − 0,01 4300 = 21. Рейтинг модели «Г»: R_Г = 8 (2 + 0) + 4 3 − 0,01 3900 = −11. Наибольший рейтинг, равный 21, имеет модель «В». Правильный ответ: 21

↑ Задание 5 № 77368 тип B5 Решите уравнение . Решение. Выполним преобразования: Ответ: −1,5.

↑ Задание 6 № 27397 тип B6

В треугольнике угол равен 90°, косинус внешнего угла при вершине равен . Найдите . Решение. так как , имеем

Ответ: 0,25.

↑ Задание 7 № 26747 тип B7 Найдите значение выражения . Решение. Выполним преобразования: .

Ответ: 2.

Задание 8 № 500035 тип B8

Н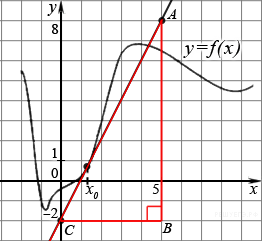 а рисунке изображены график функции и касательная к этому графику, проведённая в точке с абсциссой . Найдите значение производной функции в точке . Решение. Значение производной в точке касания равно тангенсу угла наклона касательной к оси абсцисс. Построим треугольник с вершинами в точках , и . Угол равен углу наклона касательной. Его тангенс равен отношению противолежащего катета к прилежащему: Ответ: 2.

↑ Задание 9 № 318474 тип B9

В прямоугольном параллелепипеде известны длины рёбер , , . Найдите синус угла между прямыми и . Решение. Отрезки DC и D₁C₁ лежат на параллельных прямых, поэтому искомый угол между прямыми A₁C₁ и DC равен углу между прямыми A₁C₁ и D₁C₁. Из прямоугольного треугольника A₁C₁D₁ по получаем:

Тогда для угла A₁C₁D₁ имеем: Ответ:0,6.

↑ Задание 10 № 320187 тип B10

При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98? Решение. Найдем вероятность противоположного события, состоящего в том, что цель не будет уничтожена за n выстрелов. Вероятность промахнуться при первом выстреле равна 0,6, а при каждом следующем — 0,4. Эти события независимые, вероятность их произведения равна произведению вероятности этих событий. Поэтому вероятность промахнуться при n выстрелах равна: Осталось найти наименьшее натуральное решение неравенства

Последовательно проверяя значения , равные 1, 2, 3 и т. д. находим, что искомым решением является . Следовательно, необходимо сделать 5 выстрелов. Ответ: 5.

Примечание. Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов: Р(1) = 0,6. Р(2) = Р(1)·0,4 = 0,24. Р(3) = Р(2)·0,4 = 0,096. Р(4) = Р(3)·0,4 = 0,0384; Р(5) = Р(4)·0,4 = 0,01536. Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени. Приведем другое решение. Вероятность поразить мишень равна сумме вероятностей поразить ее при первом, втором, третьем и т. д. выстрелах. Поэтому задача сводится к нахождению наименьшего натурального решения неравенства

В нашем случае неравенство решается подбором, в общем случае понадобится формула суммы геометрической прогрессии, использование которой сведет задачу к простейшему логарифмическому неравенству. Правильный ответ: 5

↑ Задание 11 № 27175 тип B11

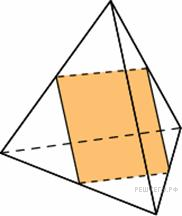
Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер. Решение. Каждая сторона сечения является серединной линией соответствующей грани, которая, как известно, в 2 раза меньше параллельной ей стороны и равна поэтому 0,5. Тогда площадь сечения .

Ответ: 0,25.

↑ Задание 12 № 28000 тип B12

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону , где – время в секундах, амплитуда В, частота /с, фаза . Датчик настроен так, что если напряжение в нeм не ниже чем В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть? Решение. Задача сводится к решению уравнения при заданных значениях амплитуды сигнала, частоты и фазы:

На протяжении первой секунды лампочка будет гореть с, то есть % времени.

Ответ: 50.

↑ Задание 13 № 99606 тип B13

Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость равна:

км/ч. Ответ: 70.

↑ Задание 14 № 26713 тип B14

Найдите точку максимума функции . Решение. Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума .

Ответ: −15.

Вопрос:Объясните пожалуйста, откуда берется (-1)? Просто не вижу отличий между предыдущими заданиями, а принцип решения разный. Спасибо.

Ответ: Мы вычисляем производную сложной функции, умножаем на коэффициент перед x.

Начало формы