Задание с1 № 485964
а) Решите уравнение . б) Укажите корни этого уравнения, принадлежащие промежутку
Решение.
а) Преобразуем уравнение:
.
Если , то из уравнения следует , что невозможно. Значит, на множестве корней уравнения . Разделим обе части уравнения на :
.
б) Составим двойное неравенство: , откуда . Следовательно, . Поэтому на данном отрезке получаем единственный корень .
Ответ: а) ; б) .
Вопрос:скажите, пожалуйста, почему sinX=0 невозможно?
Ответ: Одновременно sin(x) и cos(x) не могут равняться 0.
Задание с2 № 500013
В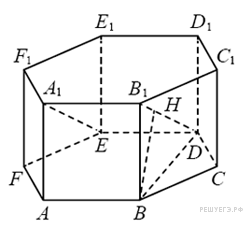
правильной шестиугольной призме
все
рёбра равны 1. Найдите расстояние от
точки В
до плоскости
.
Решение.
Прямые
и
DB
перпендикулярны прямой ED.
Плоскость
,
содержащая прямую ED,
перпендикулярна плоскости
.
Значит, искомое расстояние равно высоте
BH
прямоугольного треугольника
,
в котором
,
,
.
Тогда
.
Ответ:
Задание с3 № 500368Решить систему неравенств
Решение.
1.
Решим первое неравенство системы.
Сделаем замену
Тогда
или
откуда
находим решение второго неравенства
исходной системы:
2.
Решим второе неравенство системы.
Рассмотрим два случая.
Первый
случай:
откуда
находим:
Учитывая
условие
получаем:
Второй
случай:
Учитывая
условие
получаем:
Решение
второго неравенства исходной системы:
3.
Поскольку
получаем
решение исходной системы неравенств:
Ответ:
Вопрос:
Вопрос по поводу второго неравенства
(в отрыве от первого). Обратите внимание
на основание и содержимое логарифма.
При x =1 неравенство выполняется в части
равенства и ученик имел право рассмотреть
этот случай. Я, как учитель, согласен с
таким решением, но оно идёт в разрез
определению. Если возьмём сборник
Ершов-Голобородько, то там рассматриваются
такие случаи. Больше - нигде. И что же? В
сборниках Ященко-Семёнов это решение
не принимается. Вот так и возникают
"Чёрные дыры". Ведь х^2=2-х имеет
смысл при х=1. Не могли бы осветить эту
проблему (если можно, то не с формальной
точки зрения).
Ответ:
Дело тут в том, что уравнение
имеет
бесконечно много корней. Поэтому для
придания смысла величине
требовалось
бы дополнительное соглашение о том, что
считать этой величиной.
Задание с4 № 500369
В
треугольнике
известны
стороны:
.
Окружность, проходящая через точки
и
,
пересекает прямые
и
соответственно
в точках
и
,
отличных от вершин треугольника. Отрезок
касается
окружности, вписанной в треугольник
.
Найдите длину отрезка
.
Решение.
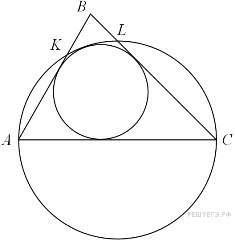Обе
точки
и
не
могут лежать вне треугольника, поскольку
в этом случае отрезок
не
может касаться вписанной окружности.
Значит, по крайней мере одна из этих
точек лежит на стороне треугольника.
Пусть обе точки
и
лежат
на сторонах треугольника. Четырехугольник
—
вписанный, следовательно,
Значит,
треугольник
подобен
треугольнику
,
так как угол
—
общий. Пусть коэффициент подобия равен
,
тогда
,
,
.
Суммы противоположных сторон описанного
четырехугольника
равны:
Подставляя
известные значения сторон, находим
.
Следовательно,
.
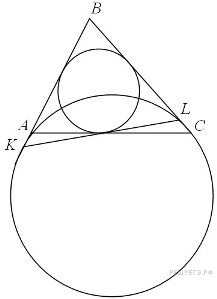
Пусть точка
лежит
на продолжении стороны
.
Углы
и
равны,
поскольку опираются на одну дугу. Значит,
треугольник
подобен
треугольнику
,
так как угол
—
общий. Более того, они описаны около
одной и той же окружности. Следовательно,
коэффициент подобия равен 1, то есть,
треугольники
и
равны,
поэтому
.
Заметим, что
и
точка
действительно
лежит на продолжении стороны
.
Если точка
лежит
на продолжении стороны
,
то
,
но, аналогично предыдущему случаю,
получаем
.
Значит, этот случай не достигается.
Ответ:
.