Результаты Вариант № 277

№ п/п	Номер	Тип	Правильный ответ
1	26636	B1	404
2	26874	B2	6
3	27653	B3	-8
4	316049	B4	75
5	77383	B5	1
6	27747	B6	64
7	26748	B7	5
8	27495	B8	1
9	910	B9	13
10	320181	B10	0,4
11	27143	B11	64
12	500148	B12	12
13	111867	B13	8
14	77429	B14	3

↑Задание 1 № 26636 тип B1 Летом килограмм клубники стоит 80 рублей. Мама купила 1 кг 200 г клубники. Сколько рублей сдачи она получит с 500 рублей? Решение. Найдем стоимость покупки: 1 кг 200 г клубники стоит 1,2   80 = 96 рублей. Значит, с 500 рублей мама получит сдачи 500 − 96 = 404 рубля.

Ответ: 404.

↑Задание 2 № 26874 тип B2

На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.

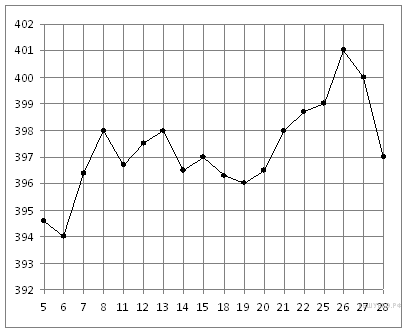
Решение. Из графика видно, что наименьшей цена была 6 марта (см. рисунок).

Ответ: 6.

↑Задание 3 № 27653 тип B3

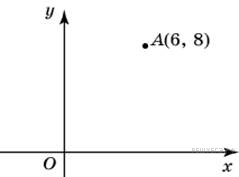Найдите ординату точки, симметричной точке A(6; 8) относительно оси Ox. Решение. Так как точка симметрична относительно оси Ox, то абсцисса равна 6, а ордината равна −8.

Ответ: −8.

Задание 4 № 316049 тип b4

Независимое агентство каждый месяц определяет рейтинги новостных сайтов на основе показателей информативности , оперативности и объективности публикаций. Каждый отдельный показатель оценивается целыми числами от −2 до 2. Итоговый рейтинг вычисляется по формуле

В таблице даны оценки каждого показателя для нескольких новостных сайтов. Определите наивысший рейтинг новостных сайтов, представленных в таблице. Запишите его в ответ, округлив до целого числа.

Сайт	Информативность	Оперативность	Объективность
VoKak.ru	2	−1	0
NashiNovosti.com	−2	1	−1
Bezvrak.ru	2	2	0
Zhizni.net	−1	−1	−2

Решение. Рассмотрим все варианты. Сайт VoKak.ru: Сайт NashiNovosti.com: Сайт Bezvrak.ru: Сайт Zhizni.net: Таким образом, наивысший рейтинг имеет сайт Bezvrak.ru, он равен 75. Ответ: 75.

↑Задание 5 № 77383 тип B5 Найдите корень уравнения: . Решение. Последовательно получаем:

Ответ: 1.

↑Задание 6 № 27747 тип B6

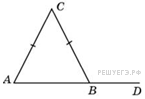В треугольнике . Внешний угол при вершине равен . Найдите угол . Ответ дайте в градусах. Решение. так как треугольник равнобедренный, то углы при его основании равны.

.Ответ: 64.

↑Задание 7 № 26748 тип B7 Найдите значение выражения . Решение. Выполним преобразования:

.

Ответ: 5.

↑Задание 8 № 27495 тип B8 На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек минимума функции на отрезке .

Решение. Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. На отрезке функция имеет одну точку минимума .

Ответ: 1.

↑Задание 9 № 910 тип B9

Высота конуса равна 12, а диаметр основания – 10. Найдите образующую конуса. Решение. образующая конуса по теореме Пифагора равна

Ответ: 13.

↑Задание 10 № 320181 тип B10 В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин? Решение. Всего туристов пять, случайным образом из них выбирают двоих. Вероятность быть выбранным равна 2 : 5 = 0,4.

Ответ: 0,4.

↑Задание 11 № 27143 тип B11

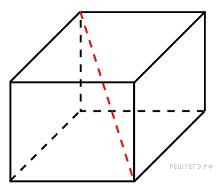Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда. Решение. Обозначим известные ребра за и , а неизвестное за . Площадь поверхности параллелепипеда выражается как

. Диагональ параллелепипеда находится как .

Выразим : .

Тогда площадь поверхности

Ответ: 64.

↑Задание 12 № 500148 тип B12 Зависимость объема спроса (единиц в месяц) на продукцию предприятия монополиста от цены (тыс. руб.) задается формулой . Выручка предприятия за месяц (тыс. руб.) вычисляется по формуле . Определите наибольшую цену , при которой месячная выручка составит 960 тыс. руб. Ответ приведите в тыс. руб. Решение. Задача сводится к решению уравнения :

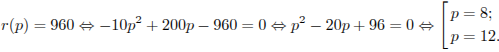Ответ: 12.

↑Задание 13 № 111867 тип B13 Грузовик перевозит партию щебня массой 60 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 4 тонны щебня. Определите, сколько тонн щебня было перевезено за пятый день, если вся работа была выполнена за 8 дней. Решение. Пусть в первый день грузовик перевез тонны щебня, во второй — , …, в последний — тонн; всего было перевезено тонн; норма перевозки увеличивалась ежедневно на тонн. Поскольку

. Имеем

.

Следовательно, за пятый день было перевезено 8 тонн щебня. Ответ: 8.

↑Задание 14 № 77429 тип B14 Найдите наименьшее значение функции на отрезке . Решение. Найдем производную заданной функции: . Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

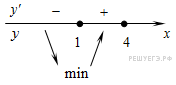
В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

.

Ответ: 3.

Начало формы