Задание с6 № 484655

Найдите все такие пары натуральных чисел a и b, что если к десятичной записи числа a приписать справа десятичную запись числа b, то получится число, большее произведения чисел a и b на 32.

Решение. , где k — число цифр в числе b, . Тогда , иначе .

Непосредственно проверяем . Соответственно: . Ответ: 12 и 8; 23 и 9.

Результаты Вариант № 412

№ п/п	Номер	Тип	Правильный ответ
1	26627	B1	34
2	500635	B2	37,9
3	27612	B3	8
4	26686	B4	10250,64
5	77371	B5	-7
6	27797	B6	8
7	26778	B7	-1
8	119974	B8	7
9	910	B9	13
10	285925	B10	0,36
11	74429	B11	729
12	500168	B12	10
13	99602	B13	22
14	77454	B14	-8

↑ Задание 1 № 26627 тип B1

Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей? Решение. С учетом наценки учебник будет стоить 170 + 0,2   170 = 204 рубля. Разделим 7000 на 204:

.

Значит, можно будет купить 34 учебника. Ответ: 34.

↑ Задание 2 № 500635 тип B2

На рисунке жирными точками показан курс японской йены, установленный Центробанком РФ, во все рабочие дни с 23 сентября по 23 октября 2010 года. По горизонтали укладываются числа месяца, по вертикали — цена японской йены в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольший курс японской йены за указанный период. Ответ дайте в рублях.

Решение. Из графика видно, что наибольший курс доллара за указанный период составил 37,9 рубля (см. рисунок).

Ответ: 37,9.

↑ Задание 3 № 27612 тип B3

Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма. Решение. Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно a и b. Тогда S = 5   a = 10   b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.

Ответ: 8.

↑ Задание 4 № 26686 тип B4

В таблице даны условия банковского вклада в трех различных банках. Предполагается, что клиент кладет на счет 10 000 рублей на срок 1 год. В каком банке к концу года вклад окажется наибольшим? В ответе укажите сумму этого вклада в рублях.

Банк	Обслуживание счета *	Процентная ставка (% годовых) **
Банк А	40 руб. в год	2
Банк Б	8 руб. в месяц	3,5
Банк В	Бесплатно	1,5

* В начале года или месяца со счета снимается указанная сумма в уплату за ведение счета ** В конце года вклад увеличивается на указанное количество процентов. Решение. Рассмотрим различные варианты. В банке A после снятия суммы в уплату за ведение счета на счету останется 10 000 − 40 = 9 960 руб. К концу года на счету окажется 9 960 + 0,02   9 960 = 10 159,2 руб. В банке Б в качестве платы за ведение счета за год снимается со счета 12   8 = 96 руб. Таким образом, проценты начисляются на сумму 10 000 − 96 = 9 904 руб. К концу года на счету окажется 9 904 + 0,035   9 904 = 10 250,64 руб. В банке В плата за ведение счета не взимается, таким образом, проценты будут начисляться на первоначальную сумму. К концу года на счету окажется 10 000 + 0,015   10 000 = 10 150 руб.

Ответ: 10 250,64.

Ваш ответ: нет ответа. Правильный ответ: 10250,64

Вопрос:Объясните, пожалуйста, процент же берется от суммы, которую вложили? Что я не так понял?

Ответ: По условиям вклада процент выплачивается на сумму, которая осталась после уплаты комиссии за обслуживание счета.

Вопрос:Прошу, уточните вопрос. Я понял ровно так же - что сначала вклад увеличивается на процент, а потом снимается сумма за обслуживание.

Ответ: Вы невнимательно прочли условие: * В начале года или месяца со счета снимается комиссия за ведение счета. ** В конце года вклад увеличивается на указанное количество процентов.

↑ Задание 5 № 77371 тип B5 Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Решение. Последовательно получаем: Ответ:  −7.

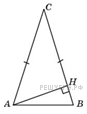↑ Задание 6 № 27797 тип B6

В треугольнике , высота равна 4, угол равен . Найдите . Решение. .

Ответ: 8.

↑ Задание 7 № 26778 тип B7 Найдите , если и . Решение. Поскольку , определяем, что . Тогда

.

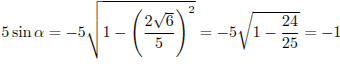Ответ: -1.

↑ Задание 8 № 119974 тип B8 Прямая является касательной к графику функции . Найдите . Решение. Условие касания графика функции и прямой задаётся системой требований:

В нашем случае имеем:

Ответ: 7.

↑ Задание 9 № 910 тип B9

Высота конуса равна 12, а диаметр основания – 10. Найдите образующую конуса. Решение. образующая конуса по теореме Пифагора равна

Ответ: 13.

↑ Задание 10 № 285925 тип B10

П еред началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Решение. В первом туре Руслан Орлов может сыграть с 26 − 1 = 25 бадминтонистами, из которых 10 − 1 = 9 из России. Значит, вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна Ответ: 0,36.

↑ Задание 11 № 74429 тип B11 Диагональ куба равна . Найдите его объем. Решение.Диагональ куба в раз больше его ребра. Поэтому ребро куба равно

Тогда объем куба   .

Ответ: 729.

↑ Задание 12 № 500168 тип B12 Зависимость объема спроса (единиц в месяц) на продукцию предприятия монополиста от цены (тыс. руб.) задается формулой . Выручка предприятия за месяц (тыс. руб.) вычисляется по формуле . Определите наибольшую цену , при которой месячная выручка составит 300 тыс. руб. Ответ приведите в тыс. руб. Решение. Задача сводится к решению уравнения :

Ответ: 10.

↑ Задание 13 № 99602 тип B13

Расстояние между пристанями и равно 120 км. Из в по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт , тотчас повернула обратно и возвратилась в . К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч. Решение. Скорость плота равна скорости течения реки 2 км/ч. Пусть км/ч – скорость яхты, тогда скорость яхты по течению равна км/ч, а скорость яхты против течения равна км/ч. Яхта, прибыв в пункт , тотчас повернула обратно и возвратилась в , а плоту понадобилось на час больше времени, чтобы пройти 24 км.

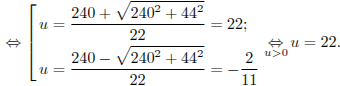
Ответ: 22.

↑ Задание 14 № 77454 тип B14 Найдите наименьшее значение функции на отрезке . Решение. Найдем производную заданной функции: Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Найденная производная неположительна на заданном отрезке, заданная функция убывает на нем, поэтому наименьшим значением функции на отрезке является .

Ответ: −8.

Начало формы