Задание с1 № 484550

Решите систему уравнений

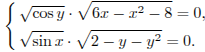
Решение.

Из неравенства получаем . 1 случай. Пусть или . Если , то ; если , то . Из второго уравнения получаем , откуда или . 2 случай. Пусть теперь . Тогда , и поэтому из первого уравнения получаем: . Учтем, что . Тогда . Из всех решений уравнения этому условию удовлетворяет только . При этом и, из второго уравнения получаем: . Из всех решений этого уравнения интервалу принадлежит только . Значит, , . Ответ: .

Задание с2 № 484577

В правильной треугольной призме , все рёбра которой равны 1, найдите расстояние между прямыми и .

Решение.

Т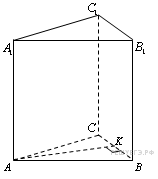 ак как прямая пересекается с прямой параллельной прямой и лежит в плоскости , параллельной , то расстояние между прямыми и равно расстоянию от прямой до плоскости .

Пусть АК — высота треугольника ABC. АК перпендикулярна , так как перпендикулярна плоскости ABC. Таким образом, искомое расстояние — длина отрезка АК. Из равностороннего треугольника ABC находим:

.

Ответ: .

Задание с3 № 484604

Решите систему неравенств

Решение.

Решим первое неравенство:

.

Осталось найти положительные решения второго неравенства. Заметим, что выражение, стоящее под знаком логарифма, не меньше 1:

.

При положительных значениях переменной справедливы неравенства и , а значит,

, и .

Тем самым, неравенство выполнено в том и только В том случае, когда оба выражения равны нулю. Следовательно,

Отрицательное решение неравенства не является решением системы. Ответ: .

Задание с4 № 500430

У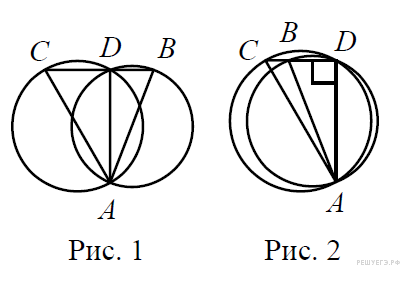 гол треугольника равен , — отличная от точка пересечения окружностей, построенных на сторонах и как на диаметрах. Известно, что . Найдите угол .

Решение.

Точка лежит на окружности с диаметром , поэтому . Аналогично, . Следовательно, точка лежит на прямой . Возможны два случая: точка лежит либо на отрезке (рис. 1), либо на продолжении отрезка за точку (рис. 2). Точка не может лежать на продолжении отрезка за точку , так как угол — острый. Положим , . Из прямоугольных треугольников и находим:

. Рассмотрим первый случай. По теореме синусов , то есть 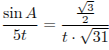, откуда . Во втором случае , откуда . Поскольку , получаем: , значит, — острый и равен или . Ответ: .

Задание с5 № 500196

Найдите все значения а, при каждом из которых неравенство выполняется для всех .

Решение.

Рассмотрим функцию . Эта функция возрастает на промежутке и убывает па промежутке . Исходное неравенство имеет вид , значит, график функции на отрезке должен находиться в пределах горизонтальной полосы: Отрезок не должен лежать на участке монотонности функции , иначе приращение на отрезке длины 5 будет не меньше 25, поэтому её график не поместится в полосе ширины 20. Следовательно, , откуда . Наибольшее значение функции на отрезке достигается либо при , либо при . Наименьшее значение функции на отрезке достигается при . Получаем систему:

,

откуда . Ответ: