Задание с6 № 500820

На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех отрицательных из них равно −8. а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них?

Решение.

Пусть среди написанных чисел положительных, отрицательных и нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому а) Заметим, что в лувой части приведенного выше равенства каждое слагаемое делится на 4, поэтому — количество целых чисел — делится на 4. По условию поэтому Таким образом, написано 44 числа. б) Приведем неравенство к виду Так как получаем, что откуда Следовательно, отрицательных чисел больше, чем положительных. в_оценка) Подставим в правую часть равенства откуда Так как получаем: то есть положительных чисел не более 17. в_пример) Приведем пример, когда положительных чисел ровно 17. Пусть на доске 17 раз написано число 4, 25 раз написано число −8 и два раза написан 0. Тогда указанный набор удовлетворяет всем условиям задачи.

Ответ:а) 44; б) отрицательных; в) 17.

Результаты Вариант № 411

№ п/п	Номер	Тип	Правильный ответ
1	24655	B1	2
2	27519	B2	7
3	27622	B3	30
4	319558	B4	1
5	77369	B5	-6
6	27362	B6	0,96
7	77389	B7	5
8	317542	B8	5
9	316554	B9	60
10	320172	B10	0,52
11	245336	B11	8
12	42869	B12	3
13	99582	B13	18
14	245178	B14	3

↑ Задание 1 № 24655 тип B1 В университетскую библиотеку привезли новые учебники по геометрии для 2—3 курсов, по 280 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 7 полок, на каждой полке помещается 30 учебников. Сколько шкафов можно полностью заполнить новыми учебниками?

Решение. Всего привезли 280   2 = 560 учебников по геометрии. В книжном шкафу помещается 30   7 = 210 учебников. Разделим 560 на 210: . Значит, полностью можно будет заполнить 2 шкафа.

Ответ: 2.

Вопрос:В двух шкафах не будет хватать место на для всех учебников. Ответ должен быть 3 шкафа?

Ответ: Полностью можно будет заполнить 2 шкафа.

↑ Задание 2 № 27519 тип B2

На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой.

Решение. Из диаграммы видно, что было 7 месяцев с температурой выше нуля (см. рисунок). Ответ: 7.

↑ Задание 3 № 27622 тип B3 Площадь остроугольного треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами. Ответ дайте в градусах. Решение. По формуле площади треугольника . Поэтому .

Поскольку угол острый, он равен Ответ: 30.

↑ Задание 4 № 319558 тип B4

Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены и оценок функциональности , качества и дизайна . Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

Модель печи	Средняя цена	Функциональность	Качество	Дизайн
А	1900	1	1	1
Б	5900	4	1	2
В	3800	0	0	1
Г	4100	2	0	4

Решение. Рассмотрим все варианты. Модель А: Модель Б: Модель В: Модель Г: Таким образом, наивысший рейтинг имеет модель А. Он равен 1.

Ответ: 1.

↑ Задание 5 № 77369 тип B5 Решите уравнение .

Решение. Используем формулы квадрата разности и квадрата суммы:

Ответ: −6.

↑ Задание 6 № 27362 тип B6

В треугольнике угол равен 90°, . Найдите синус внешнего угла при вершине . Решение. так как ,

имеем

Ответ: 0,96.

↑ Задание 7 № 77389 тип B7 Найдите значение выражения . Решение. Выполним преобразования: . Ответ: 5.

↑ Задание 8 № 317542 тип B8

На рисунке изображён график производной функции и восемь точек на оси абсцисс: , . В скольких из этих точек функция убывает?

Решение. Убыванию дифференцируемой функции соответствуют отрицательные значения её производной. Производная отрицательна в точках Следовательно, таких точек 5.

Ответ:5.

↑ Задание 9 № 316554 тип B9

В кубе найдите угол между прямыми и . Ответ дайте в градусах. Решение. Поскольку — куб, каждая из его граней является квадратом. Диагонали этих квадратов равны, поэтому Тогда треугольник  — равносторонний, следовательно, искомый угол равен 60°.

Ответ:60.

↑ Задание 10 № 320172 тип B10

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. Решение.Рассмотрим события

А = кофе закончится в первом автомате, В = кофе закончится во втором автомате.

Тогда A·B = кофе закончится в обоих автоматах, A + B = кофе закончится хотя бы в одном автомате. По условию P(A) = P(B) = 0,3; P(A·B) = 0,12. События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48. Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52. Ответ: 0,52. Приведем другое решение. Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятость х = 0,52. Примечание. Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако по условию эта вероятность равна 0,12.

↑ Задание 11 № 245336 тип B11

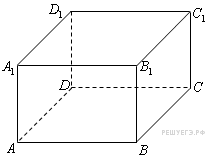
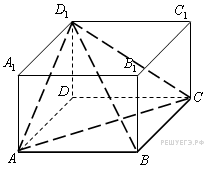Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , . Решение. Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому

Ответ: 8.

↑ Задание 12 № 42869 тип B12

Уравнение процесса, в котором участвовал газ, записывается в виде , где  (Па) — давление в газе,  — объeм газа в кубических метрах,  — положительная константа. При каком наименьшем значении константы увеличение в 3 раза объeма газа, участвующего в этом процессе, приводит к уменьшению давления не менее, чем в 27 раз? Решение. Пусть и – начальные, а и – конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства , причем : .

Значит, наименьшее значение константы равно 3. Ответ: 3.

↑ Задание 13 № 99582 тип B13

Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров. Решение. В первый день турист прошел км, во второй – , …, в последний – км. Всего он прошел км. Каждый день турист проходил больше, чем в предыдущий день, на км, , дней. Таким образом, км.

Тогда за третий день турист прошел км. Ответ: 18.

↑ Задание 14 № 245178 тип B14 Найдите точку минимума функции . Решение. Квадратный трехчлен с положительным старшим коэффициентом достигает минимума в точке , в нашем случае — в точке 3. Поскольку функция возрастает, и заданная функция определена в точке 3, она также достигает в ней минимума.

Ответ: 3.

Начало формы