Задание с1 № 485977

а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку

Решение.

а) Разложим левую часть на множители:

Уравнение , не имеет корней. Имеем

Если , то , это невозможно. Это однородное уравнение первой степени, разделим обе его части на . Получаем:

б) Отрезку принадлежат корни и (см. рис.)

Ответ: а) где , б) и

Вопрос:Куда перед синусом делась двойка, когда мы сгруппировали уравнение?

Ответ: Обе части уравнения разделили на 2.

Задание с2 № 486000

В правильной треугольной пирамиде с основанием точка — середина ребра точка  — середина ребра Найдите угол между плоскостями и если

Решение.

Проведем перпендикуляр к — середина Из точки опустим перпендикуляр на плоскость основания. Точка лежит на медиане треугольника Прямая параллельна прямой пересечения плоскостей и и Следовательно, — линейный угол искомого угла между плоскостями. Далее находим:

Откуда Ответ:

Задание с3 № 500020

Решите систему неравенств

Решение.

1. Решим первое неравенство системы. Сделаем замену .

; ; .

Тогда , откуда находим решение первого неравенства системы: . 2. Решим второе неравенство системы. Рассмотрим два случая. Первый случай: .

; ; ; .

Учитывая условие , получаем: . Второй случай: .

; ; ; .

Учитывая условие , получаем ; . Решение второго неравенства системы: ; ; . 3. Решение исходной системы неравенств: ; ; .

Ответ: ; ; .

Задание с4 № 485945

Точка лежит на отрезке На окружности с диаметром взята точка удаленная от точек и на расстояния 40, 29 и 30 соответственно. Найдите площадь треугольника

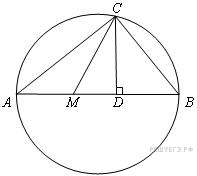Решение.

Точка лежит на окружности с диаметром поэтому По теореме Пифагора Пусть — высота треугольника Тогда:

Из прямоугольного треугольника находим:

Если точка лежит между точками и , то Следовательно,

Если точка лежит между и , то . Следовательно,

Ответ:

Задание с5 № 484642

Найдите все значения параметра а, при каждом из которых система уравнений имеет а) ровно четыре решения, б) ровно 8 решений.

Решение.

Преобразуем данную систему:

Сделав замену переменной , получаем систему

Заметим, что количество решений полученной системы совпадает с количеством решений исходной системы. Построим графики уравнений (1) и (2) в системе координат Oxt. График первого уравнения — ромб, диагонали которого, равные 24 и 10, лежат соответственно на осях х и Ot, а графиком второго уравнения является окружность с центром в начале координат и радиусом (см. рисунок).

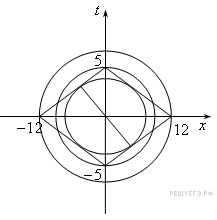
Графики уравнений системы имеют ровно четыре общих точки, и, следовательно, система имеет ровно четыре решения, тогда и только тогда, когда окружность либо вписана в ромб, либо ее радиус удовлетворяет соотношению , где  — половины меньшей и большей диагоналей ромба соответственно. Радиус вписанной в ромб окружности равен высоте прямоугольного треугольника с катетами, равными 5 и 12, откуда

Таким образом, система имеет 4 ровно решения, если или , откуда или Графики имеют 8 общих точек, если радиус окружности удовлетворяет условию , где  — радиус окружности, вписанной в ромб. Тогда , откуда

.

Ответ: а) б) .