Задание с6 № 500005

На доске написано число 7. Раз в минуту Вася дописывает на доску одно число: либо вдвое большее какого-то из чисел на доске, либо равное сумме каких-то двух чисел, написанных на доске (таким образом, через одну минуту на доске появится второе число, через две ― третье и т.д.). а) Может ли в какой-то момент на доске оказаться число 2012? б) Может ли в какой-то момент сумма всех чисел на доске равняться 63? в) Через какое наименьшее время на доске может появиться число 784?

Решение.

а) Заметим, что каждое число на доске будет делиться на 7. Действительно, исходное число делится на 7, в случае удвоения числа делящегося на 7, получится число, делящееся на 7. А при сложении чисел, делящихся на 7, также получится число, делящееся на 7. Таким образом, все числа на доске будут делиться на 7, а 2012 на 7 не делится, следовательно, оно не может появиться на доске. б) Да, может. Пример: 7, 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7). Сумма полученных 5 чисел равна 63. Замечание. В условии не сказано, что одно число нельзя удваивать несколько раз. в) Как было замечено в пункте а, все числа на доске будут делиться на 7. Рассмотрим аналогичную задачу, разделив исходное число 7 и то число, которое нужно получить, т.е. 784, на 7. От этого количество операций не изменится. Таким образом, достаточно за наименьшее количество операций получить число 112, начав с числа 1. Заметим, что наибольшее число, которое может получиться на доске через 6 минут, равно 64 (если Вася каждый раз будет удваивать текущее наибольшее число). Следовательно, если в первые 6 минут Вася каждый раз удваивал наибольшее число на доске, то число 112 нельзя получить за 7 минут: если число 64 удвоить, то получится 128, а если прибавить к нему число, не превосходящее 32, то 112 не получится. В том случае, если в течение первых 6 минут Вася использовал хотя бы одно сложение вместо удвоения, то при первом использовании сложения наибольшее число, записанное на доске увеличилось не более, чем в полтора раза: действительно, в этом случае самый большой результат получится тогда, когда мы к максимальному на данный момент числу прибавим второе по величине, то есть, его половину (напомним, что мы рассматриваем первый случай сложения, то есть до этого были только удвоения). Таким образом, даже если в течение первых 7 минут сделано 6 удвоений и одно сложение (в некотором порядке), то наибольшее число, которое может получиться, равно , что меньше 112. Итак, за 7 минут число 112 получить невозможно. Приведем пример, как его получить за 8 минут: 1 1,2 1,2,4 1,2,4,8 1,2,4,8,16 1,2,4,8,16,32 1,2,4,8,16,32,64 1,2,4,8,16,32,64,96 (96 = 64 + 32 ) 1,2,4,8,16,32,64,96,112 (112 = 96 + 16 ).

Ответ: а) нет; б) да; в) 8 минут.

Вариант № 410

№ п/п	Номер	Тип	Правильный ответ
1	77346	B1	20
2	27527	B2	14
3	27618	B3	6
4	26672	B4	479700
5	100757	B5	-1
6	27846	B6	4
7	62771	B7	8
8	317540	B8	7
9	284355	B9	1
10	320199	B10	0,408
11	27124	B11	2
12	28003	B12	30
13	99615	B13	10
14	26723	B14	10

↑ Задание 1 № 77346 тип B1 Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена? Решение. Цену на телефон снизили на 3500 − 2800 = 700 рублей. Разделим 700 на 3500: .

Значит, цену снизили на 20%. Ответ: 20.

↑ Задание 2 № 27527 тип B2

Н а рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.

Решение. Из 16 наблюдений, представленных на графике, 2 дня выпадало более 3 мм осадков. Поэтому 14 дней выпадало менее 3 мм осадков.

Ответ: 14.

↑ Задание 3 № 27618 тип B3

Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет. Решение. Пусть x — меньший катет, тогда x + 2 — больший. Площадь прямоугольного треугольника равна половине произведения катетов:

Ответ: 6.

↑ Задание 4 № 26672 тип B4

Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?

Перевозчик	Стоимость перевозки одним автомобилем (руб. на 100 км)	Грузоподъемность автомобилей (тонн)
А	3200	3,5
Б	4100	5
В	9500	12

Решение.Рассмотрим все варианты. Для перевозки 45 тонн груза перевозчику A понадобится 13 автомобилей. Стоимость перевозки каждым из них составит 32   1300 = 41 600 руб. Полная стоимость перевозки 41 600   13 = 540 800 руб. Для перевозки 45 тонн груза перевозчику Б понадобится 9 автомобилей. Стоимость перевозки каждым из них составит 41   1300 = 53 300 руб. Полная стоимость перевозки 53 300   9 = 479 700 руб. Для перевозки 45 тонн груза перевозчику В понадобится 4 автомобиля. Стоимость перевозки каждым из них составит 95   1300 = 123 500 руб. полная стоимость перевозки 123 500   4 = 494 000 руб. Стоимость самой дешевой перевозки составит 479 700 руб. Ответ: 479 700.

↑ Задание 5 № 100757 тип B5 Решите уравнение .

Решение. Квадраты чисел равны, если сами числа равны или противоположны. Поэтому:

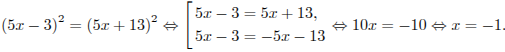Ответ: −1.

↑ Задание 6 № 27846 тип B6

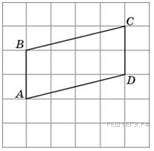Найдите высоту параллелограмма , опущенную на сторону , если стороны квадратных клеток равны 1. Решение. проведем высоту из вершины . По рисунку находим ее высоту.

Ответ: 4.

↑ Задание 7 № 62771 тип B7 Найдите значение выражения .

Решение. Выполним преобразования:

.Ответ: 8.

↑ Задание 8 № 317540 тип B8

На рисунке изображён график функции и двенадцать точек на оси абсцисс: , , , , . В скольких из этих точек производная функции отрицательна?

Решение. Отрицательным значениям производной соответствуют интервалы, на которых функция убывает. В этих интервалах лежат точки Таких точек 7.

Ответ:7.

↑ Задание 9 № 284355 тип B9 В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна , . Найдите объем пирамиды. Решение. Основание пирамиды — равносторонний треугольник, поэтому, является центром основания, а — высотой пирамиды . Тогда .

Ответ: 1.

↑ Задание 10 № 320199 тип B10

Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей. Решение. Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов. Пусть A, B, C и D — это события, в которых З. сдает соответственно математику, русский, иностранный и обществознание не менее, чем на 70 баллов. Тогда поскольку

для вероятности поступления имеем:

Ответ: 0,408.

↑ Задание 11 № 27124 тип B11

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду? Решение. Объемы данных конусов соотносятся как площади их оснований, и, следовательно, как квадраты их диаметров. Диаметр вписанного конуса равен стороне квадрата, диаметр описанного – диагонали квадрата, длина которой равна   длины стороны. Поэтому объем описанного конуса в 2 раза больше объема вписанного.

Ответ: 2.

↑ Задание 12 № 28003 тип B12

Небольшой мячик бросают под острым углом к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой , где м/с – начальная скорость мячика, а – ускорение свободного падения (считайте м/с ). При каком наименьшем значении угла (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м? Решение. Задача сводится к решению неравенства на интервале при заданных значениях начальной скорости . и ускорения свободного падения :

.

Ответ: 30.

↑ Задание 13 № 99615 тип B13

Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно? Решение. Обозначим объем бака за 1. Тогда три насоса, работая вместе, заполнят бак за

минут.

Ответ: 10.

Приведем другое решение. Первый насос за минуту наполняет одну двадцатую бака, второй — одну тридцатую, третий — одну шестидесятую. Работая вместе, за минуту они наполнят шесть шестидесятых или одну десятую бака. Значит, весь бак насосы наполнят за 10 минут. Приведем другое решение. За один час первый насос наполнит 3 бака, второй — 2 бака, а третий — 1 бак. Работая вместе, за один час они 6 баков. Значит, один бак насосы наполнят в шесть раз быстрее, т. е. за 10 минут.

↑ Задание 14 № 26723 тип B14 Найдите точку минимума функции . Решение. Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

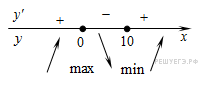Искомая точка минимума . Ответ: 10.

Начало формы