Задание с1 № 484553

Решите уравнение .

Решение.

Уравнение равносильно системе

Уравнение системы приводится к виду , откуда или . Уравнение не имеет решений. Учитывая, что котангенс должен быть отрицательным, получаем: . Ответ: .

Задание с2 № 500024

В прямоугольном параллелепипеде , . Найдите угол между прямой и плоскостью .

Решение.

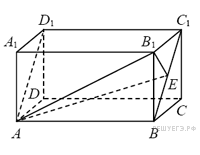Плоскости и перпендикулярны. Перпендикуляр из точки к плоскости лежит в плоскости и пересекает прямую в точке E. Значит, искомый угол равен углу . В прямоугольном треугольнике катет , гипотенуза . Поэтому

.

Тогда . Ответ: . Примечание. Возможны другие формы ответа: .

Задание с3 № 485944

Решите систему неравенств

Решение.

Решим первое неравенство системы:

Решения: или Решим второе неравенство системы:

Сделаем замену Тогда Вернемся к исходной переменной:

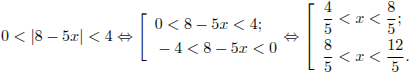
Вернемся к системе:

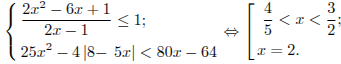
Ответ: .

Задание с4 № 484616

Окружность S проходит через вершину C прямого угла и пресекает его стороны в точках, удаленных от вершины C на расстояния 6 и 8. Найдите радиус окружности, вписанной в данный угол и касающийся окружности S.

Решение.

Пусть окружность S с центром O и радиусом R пересекает стороны данного прямого угла в точках A и B, , искомая окружность с центром Q касается сторон и BC угла ACB в точках N и K соответственно, а окружности S — в точке M.

Точка O — центр окружности, описанной около прямоугольного треугольника ABC, поэтому O — середина его гипотенузы AB.

.

Линия центров двух касающихся окружностей проходит через точку их касания, поэтому точки M, O и Q лежат на одной прямой. Опустим перпендикуляр OH из центра окружности S на прямую BC. Тогда OH — средняя линия треугольника ABC поэтому и , а т.к. центр окружности, вписанной в угол, лежит на его биссектрисе, то , поэтому . Опустим перпендикуляр QF из центра искомой окружности на прямую OH. Тогда

.

Предположим, что искомая окружность и окружность касаются внутренним образом. Тогда

.

Рассмотрим прямоугольный треугольник OFQ. По теореме Пифагора или

откуда находим, что .

Если же искомая окружность касается данной внешним образом, то

.

Тогда из соответствующего уравнения находим, что . Ответ: 4 или 24.

Задание с5 № 500016

Найдите все значения а, при каждом из которых наименьшее значение функции на множестве не менее 6.

Решение.

Графиком функции является парабола, ветви которой направлены вверх, а вершина имеет координаты . Значит, минимум функции на всей числовой оси достигается при . На множестве эта функция достигает наименьшего значения либо в точке , если эта точка принадлежит множеству, либо в одной из граничных точек . Если наименьшее значение функции не меньше 6, то и всякое значение функции не меньше 6. В частности,

откуда получаем систему неравенств

решениями которой являются . При имеем: , значит наименьшее значение функции достигается в точке и , что удовлетворяет условию задачи. При имеем: , значит, наименьшее значение функции достигается в одной из граничных точек , в которых значение функции не меньше 6. При имеем: , значит, наименьшее значение функции достигается в точке и , что не удовлетворяет условию задачи.

Ответ: .