Задание с1 № 485973
Дано
уравнение
.
А) Решите уравнение.
Б) Укажите
корни уравнения, принадлежащие отрезку
.
Решение.
а) Преобразуем уравнение:
Получаем:
или
откуда
или
б)
С помощью числовой окружности отберем
корни на отрезке
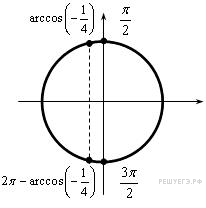
Ответ:
а)
б)
Задание с2 № 484560
В правильной треугольной SABC пирамиде с основанием ABC известны ребра . Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC.
Решение.
Пусть N — середина ребра BC, а M — середина AS. Прямая AS проецируется на плоскость основания в прямую AN. Поэтому проекция точки M — точка — лежит на отрезке AN. Значит, прямая AN является проекцией прямой AM, следовательно, угол — искомый. Поскольку , где O — центр основания, — средняя линяя треугольника SAO.
Тогда
Кроме того,
Из прямоугольного треугольника находим:
.
Ответ: .
Задание с3 № 485969
Решите систему
Решение.
Решим первое неравенство
2. Решим второе неравенство: . Значит, или 3. Решением системы является общая часть решений двух неравенств. Поскольку , получаем:
, или .
Ответ: , , .
Задание с4 № 500003
Дан
треугольник АВС.
Точка Е
на прямой АС
выбрана так, что треугольник АВЕ, площадь
которого равна 14, ― равнобедренный
с основанием АЕ
и высотой BD.
Найдите площадь треугольника АВС,
если известно, что
и
.
Решение.
Введем
следующие обозначения:
,
,
.
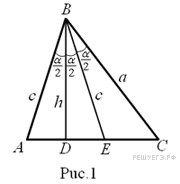1
случай (точка
E
лежит между точками A
и С,
см. рис. 1).
1. Треугольник АВЕ ―
равнобедренный, поэтому
,
а значит,
.
2. Углы ABE
и CBD
треугольников ABE
и CBD
равны. Следовательно,
,
откуда
.
3. Поскольку
,
получаем:
.
4. Окончательно находим:
.
2
случай (точка
A
лежит между точками E
и С
(см. рис. 2).
Аналогично случаю 1
находим
.
Ответ: 25 или 39.
Задание с5 № 500471
Найдите все значения , при каждом из которых наименьшее значение функции
на
множестве
не
меньше 6.
Решение.
Графиком
функции
является
парабола, ветви которой направлены
вверх, а вершина имеет координаты
.
Значит, минимум функции
на
всей числовой оси достигается при
.
На множестве
эта
функция достигает наименьшего значения
либо в точке
,
если эта точка принадлежит множеству,
либо в одной из граничных точек
Если
наименьшее значение функции не меньше
6, то и всякое значение функции не меньше
6. В частности,
откуда получаем систему неравенств
.
решениями которой являются
;
;
.
При
имеем:
,
значит, наименьшее значение функции
достигается в точке
и
,
что не удовлетворяет условию задачи.
При
имеем:
,
значит, наименьшее значение функции
достигается в одной из граничных точек
,
в которых значение функции не меньше
6.
При
имеем:
,
значит, наименьшее значение функции
достигается в точке
и
,
что не удовлетворяет условию задачи.
Ответ:
;
.
Задание с6 № 484656
Найдутся ли хотя бы три десятизначных числа, делящиеся на 11, в записи каждого из которых использованы все цифры от 0 до 9?
Решение.
Число делится на 11 тогда и только тогда, когда разность между суммами его цифр, стоящих на нечетных и на четных местах, делится на 11. Запишем все цифры подряд: 9876543210. В написанном числе указанная разность сумм равна 5. Меняя местами, например, 5 и 8, мы одну сумму увеличиваем на 3, а другую уменьшаем на 3. Значит, разность между суммами его цифр, стоящих на нечетных и на четных местах, становится равной 11. Меняя местами, например, 4 и 7, или 3 и 6, получаем требуемые примеры. Примечание: в задаче не требуется нахождение всех чисел, обладающих указанным свойством. Ответ: найдутся.
Конец формы
Конец формы
Конец фо