Задание с6 № 500017

Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9 по одному записываю на 8 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться?

Решение.

а) Среди восьми данных чисел нет противоположных. Значит, сумма чисел на каждой карточке не равна 0. Поэтому всё произведение не может равняться нулю. б) Среди восьми данных чисел пять нечётных. Значит, на какой-то карточке попадётся два нечётных числа, и их сумма чётная. Поэтому всё произведение чётно и не может равняться 1. в) Среди восьми данных чисел пять нечётных. Значит, хотя бы на двух карточках с обеих сторон написаны нечётные числа, и сумма чисел на каждой из этих карточек чётная. Поэтому всё произведение делится на 4. Наименьшее целое положительное число, делящееся на 4, это 4. Оно получается при следующем наборе пар чисел на карточках: (1; -2); (-2; 1); (-3; 4); (4; -3); (-5; 7); (7; -5); (-8; 9); (9; -8).

Ответ: а) нет; б) нет; в) 4.

Вариант № 408

№ п/п	Номер	Тип	Правильный ответ
1	26643	B1	10875
2	27510	B2	6
3	27545	B3	12
4	500140	B4	200
5	26653	B5	4
6	27931	B6	4
7	26840	B7	0
8	317541	B8	3
9	926	B9	2
10	282854	B10	0,5
11	27188	B11	7
12	27961	B12	90
13	99581	B13	65
14	77465	B14	9

↑ Задание 1 № 26643 тип B1

Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12 500 рублей. Сколько рублей он получит после вычета налога на доходы? Решение. Налог на зарплату Ивана Кузьмича составит 12 500   0,13 = 1625 рублей. Значит, после вычета налога на доходы он получит: 12 500 − 1625 = 10 875 рублей.

Ответ: 10 875.

↑ Задание 2 № 27510 тип B2

На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года. Ответ дайте в градусах Цельсия. Решение. Из графика видно, что наименьшая среднемесячная температура в период с пятого по двенадцатый месяц (с мая по декабрь) составляла 6 °C (см. рисунок). Ответ: 6.

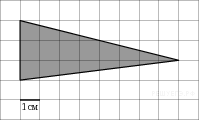
↑ Задание 3 № 27545 тип B3

На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение. Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому

см². Ответ: 12.

↑ Задание 4 № 500140 тип B4

Телефонная компания предоставляет на выбор три тарифных плана. Абонент выбрал самый дешевый тарифный план, исходя из предположения, что длительность телефонных разговоров составляет 700 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 700 минутам? Ответ дайте в рублях.

Тарифный план	Абонентская плата (в месяц)	Плата за 1 минуту разговора
«Повременный»	нет	0,35 руб.
«Комбинированный»	130 руб. за 320 мин.	0,3 руб. (сверх 320 мин. в месяц)
«Безлимитный»	200 руб.	–

Решение. Рассмотрим три случая. На тарифном плане «Повременный» ежемесячная плата будет равна оплате за 700 мин. 700   0,35 = 245 руб. На тарифном плане «Комбинированный» ежемесячная плата будет складываться из абонентской 130 руб. и платы за 380 мин. сверх тарифа 380   0,3 = 114 руб. и будет составлять 130 + 114 = 244 руб. На тарифном плане «Безлимитный» ежемесячная плата будет равна 200 рублям. Стоимость самого дешевого варианта составляет 200 рублей. Ответ: 200.

↑ Задание 5 № 26653 тип B5 Найдите корень уравнения . Решение. Перейдем к одному основанию степени: .

Ответ: 4.

↑ Задание 6 № 27931 тип B6

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу этого треугольника. В ответе укажите . Решение. Пусть длина катетов равна , тогда длина гипотенузы равна , а радиус вписанной окружности, вычисляемый по формуле , равен .

По условию , откуда .

Требовалось найти , имеем: . Ответ: 4.

Вопрос:А почему r=0,5(a+b-c), ведь по формуле r=S/p?

Ответ:Это свойство прямоугольного треугольника.

↑ Задание 7 № 26840 тип B7 Найдите , если . Решение.Подставим аргументы в формулу, задающую функцию: . Следовательно, . Ответ: 0.

↑ Задание 8 № 317541 тип B8

На рисунке изображён график производной функции и восемь точек на оси абсцисс: , . В скольких из этих точек функция возрастает?

Решение. Возрастанию дифференцируемой функции соответствуют положительные значения её производной. Производная положительна в точках Таких точек 3. Ответ:3.

↑ Задание 9 № 926 тип B9

П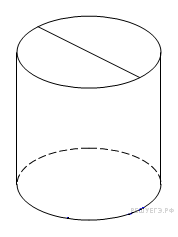 лощадь боковой поверхности цилиндра равна 18 , а диаметр основания равен 9. Найдите высоту цилиндра. Решение. высота цилиндра равна

Ответ: 2.

↑ Задание 10 № 282854 тип B10 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение. Равновозможны 4 исхода эксперимента: орел-орел, орел-решка, решка-орел, решка-решка. Орел выпадает ровно один раз в двух случаях: орел-решка и решка-орел. Поэтому вероятность того, что орел выпадет ровно 1 раз, равна .

Ответ: 0,5.

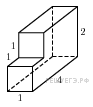
↑ Задание 11 № 27188 тип B11

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение. Объем данного многогранника равен сумме объемов параллелепипедов с ребрами 2, 3, 1 и 1, 1, 1:

. Ответ: 7.

↑ Задание 12 № 27961 тип B12

Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой , где  м , – постоянные параметры, – смещение камня по горизонтали, – высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра? Решение. Задача сводится к решению неравенства : при заданных значениях параметров a и b:

м.

Камни будут перелетать крепостную стену на высоте не менее 1 метра, если камнеметательная машина будет находиться на расстоянии от 10 до 90 метров от этой стены. Наибольшее расстояние – 90 метров.

Ответ: 90.

↑ Задание 13 № 99581 тип B13

Васе надо решить 490 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней. Решение. В первый день Вася решил задач, в последний — задач. Всего надо решить задач. Поскольку , где имеем: .

Тогда задач.Ответ: 65.

Добрый день! Мои ученики обнаружили, что число задач, на которое Вася ежедневно решает больше, — это дробное число. Действительно, a_1 = 5, a_14 = 65, поэтому разность d = (65 − 5)/(14 − 1) = 60/13, что противоречит смыслу задачи. Ответ:Действительно, условие необходимо корректировать. Мы свяжемся с разработчиками ЕГЭ и внесём изменения в задачу. Большое спасибо.

↑ Задание 14 № 77465 тип B14 Найдите точку максимума функции . Решение. Найдем производную заданной функции: .

Найдем нули производной: .

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума . Ответ: 9.

Начало формы