Задание с1 № 485996
Дано
уравнение
А)
Решите уравнение.
Б) Укажите корни
уравнения, принадлежащие отрезку
Решение.
А) Преобразуем уравнение:
Получаем:
или
Отсюда
или
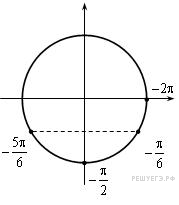Б)
С помощью числовой окружности отберем
корни на отрезке
Это
числа
Ответ:
A)
Б)
Ваша оценка (баллов):
Вопрос: При решении уравнения sin x = -1/2. По первой формуле x1=arcsin(-1/2)+2Пn вопросов нет, а с нахождением второго корня есть вопрос: x2= П-arcsin(-1/2)+2Пn, значит, x2= 7П/6+2Пn? Заранее благодарен!
Ответ:Серии 7п/6 + 2пk и −5п/6 + 2пk одинаковы. Для того, чтобы отбирать корни, нам удобнее второе представление.
Задание с2 № 484574
Дана
правильная треугольная пирамида DABC
с вершиной D.
Сторона основания пирамиды равна
,
высота равна
.
Найдите расстояние от середины бокового
ребра BD
до прямой МТ,
где точки М
и Т —
середины ребер АС
и AВ
соответственно.
Решение.
Пусть
Q —
середина ребра CD,
P —
середина ребра ВD.
По теореме о средней линии треугольника
;
следовательно, точки М,
Т,
Р,
Q
лежат в одной плоскости.
,
следовательно, точки М,
Т,
Р,
Q
являются вершинами параллелограмма.
Кроме того,
,
а по теореме о трёх перпендикулярах
(так как
),
поэтому этот параллелограмм —
прямоугольник. Значит, искомое расстояние
есть длина отрезка РТ.
Отрезок АО
равен
.
По теореме Пифагора
;
а
.
Ответ:
.
Задание с3 № 485951
Решите неравенство
Решение.
1
случай. Если
,
то
или
При
этих значениях x
выражение
имеет
смысл, поэтому числа 0 и 6 являются
решениями неравенства.
2 случай.
Если
,
то
и
тогда
С
помощью метода интервалов получаем:
;
или
.
Учитывая условие
,
находим:
или
Добавляя
точки
и
находим
все решения заданного неравенства:
,
,
Ответ:
Задание с4 № 485949
Прямая,
перпендикулярная гипотенузе прямоугольного
треугольника, отсекает от него
четырёхугольник, в который можно вписать
окружность. Найдите радиус окружности,
если отрезок этой прямой, заключённый
внутри треугольника, равен 14, а отношение
катетов треугольника равно
.
Решение.
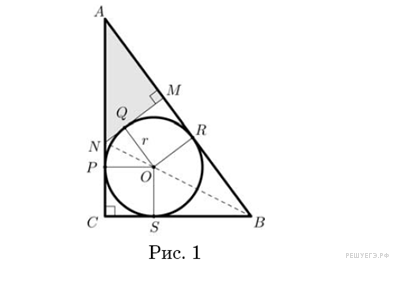Введем
обозначения как показано на рисунке:
предположим, что отрезок отсекает от
треугольника
треугольник
,
обозначим точки касания окружности и
прямых
(см.
рис. 1). Так как
и
—
квадраты,
,
где
—
радиус окружности. Кроме того,
Значит,
.
Поскольку
–
биссектриса угла, треугольники
и
равны
по гипотенузе и острому углу.
Пусть
,
а
,
тогда по теореме Пифагора находим
гипотенузу
,
откуда
.
Из подобия треугольников
и
получаем:
,
тогда
,
откуда
.
Найдём радиус окружности:
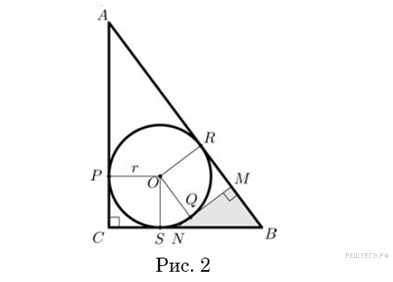Если
отрезок отсекает треугольник
(рис.
2), то, рассуждая аналогично, находим, что
Из
подобия треугольников
и
следует
откуда
получаем
и
.
В этом случае
Ответ:
8 или 12,25.
Задание с5 № 484644
Найти все значения а, при каждом из которых функция имеет более двух точек экстремума.
Решение.
1. Функция f имеет вид а) при : , поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии ; б) при : , поэтому ее график есть часть параболы с ветвями, направленными вверх, и осью симметрии . Все возможные виды графиков функции показаны на рисунках:
Графики обеих квадратичных функции проходят через точку . 3. Функция имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1):
.
Ответ: ; .