Результаты Вариант № 276

№ п/п	Номер	Тип	Правильный ответ
1	77343	B1	1296
2	263597	B2	19
3	27604	B3	14
4	246261	B4	3534
5	26656	B5	3
6	27903	B6	2
7	26861	B7	7
8	122715	B8	8
9	284349	B9	4
10	320201	B10	0,027
11	27122	B11	72
12	500039	B12	10
13	99615	B13	10
14	245179	B14	2

↑Задание 1 № 77343 тип B1 Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки? Решение. За 60 тетрадей покупатель заплатил бы 60   24 = 1440 рублей. Скидка составит 10%, т. е. 144 рубля. Значит, покупатель заплатит 1440 − 144 = 1296 рублей. О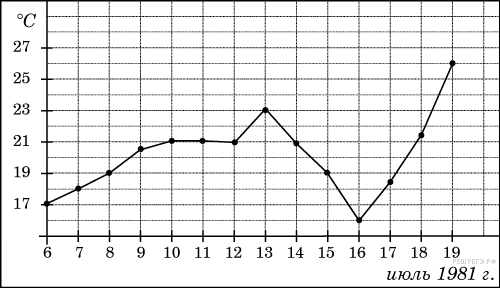 твет: 1296.

↑Задание 2 № 263597 тип B2 На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какая была температура 15 июля. Ответ дайте в градусах Цельсия.

Решение. Из графика видно, что 15 июля в Бресте было 19 градусов тепла. Ответ: 19.

↑Задание 3 № 27604 тип B3 Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника. Решение. Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, вторая равна b. Площадь и периметр прямоугольника будут соответственно равны S = a   b = 98, P = 2   a + 2   b = 42. Решая одновременно эти два уравнения, получаем, что a₁ = 7, a₂ = 14, b₁ = 14, b₂ = 7. Поэтому большая сторона равна 14. Ответ: 14.

Задание 4 № 246261 тип B4

В среднем гражданин А. в дневное время расходует 125 кВт   ч электроэнергии в месяц, а в ночное время — 155 кВт   ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,6 руб. за кВт   ч. Год назад А. установил двухтарифныйсчeтчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,6 руб. за кВт   ч, а ночной расход оплачивается по тарифу 0,7 руб. за кВт   ч. В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.

Решение. Рассмотрим оба типа счётчиков. При использовании однотарифного счётчика, гражданин А. платил в месяц

(125 кВт   ч + 155 кВт   ч) 2,6 руб. за 1 кВт   ч = 728 руб.

Поэтому за 12 месяцев он платил 728  1 2 = 8736 руб. При использовании двухтарифного счётчика, гражданин А. платит в месяц

125 кВт ч 2,6 руб. + 155 кВт ч 0,7 руб. = 433,5 руб.

Поэтому за 12 месяцев он заплатит 433,5 руб.   12 = 5202 руб. Установка нового типа счётчика позволяет экономить 8736 руб. − 5202 руб. = 3534 руб. в год.

↑Задание 5 № 26656 тип B5 Найдите корень уравнения . Решение. Возведем в квадрат: Ответ: 3.

↑ Задание 6 № 27903 тип B6

Н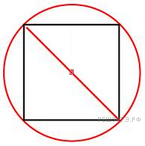 айдите радиус окружности, описанной около квадрата со стороной, равной . Решение. угол является прямым, он опирается на диагональ которая является диаметром.

Ответ: 2.

↑Задание 7 № 26861 тип B7 Найдите значение выражения . Решение. Выполним преобразования: .

Ответ: 7.

↑Задание 8 № 122715 тип B8 Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 3 с. Решение. Найдем закон изменения скорости: .

Тогда находим: м/с. Ответ: 8.

↑

Задание 9 № 284349 тип B9 В правильной четырехугольной пирамиде точка  — центр основания, вершина, , . Найдите длину отрезка . Решение. Рассмотрим треугольник . Он прямоугольный, т. к. — высота, она перпендикулярна основанию , а значит и прямой . Тогда по теореме Пифагора

. Ответ: 4.

Задание 10 № 320201 тип B10

В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга). Решение. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна

Ответ: 0,027.

↑ Задание 11 № 27122 тип B11

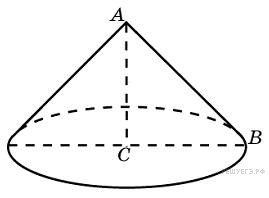
Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем, деленный на . Решение. Треугольник – так же равнобедренный, т.к. углы при основании . Тогда радиус основания равен 6, и объем конуса, деленный на :

Ответ: 72.

↑Задание 12 № 500039 тип B12 В ходе распада радиоактивного изотопа, его масса уменьшается по закону где  (мг) — начальная масса изотопа, (мин) — время, прошедшее от начального момента, (мин) — период полураспада в минутах. В начальный момент времени масса изотопа мг. Период его полураспада  мин. Через сколько минут масса изотопа будет равна 12,5 мг? Решение. Задача сводится к решению уравнения при заданных значениях параметров  мг и  мин:

мин.

Ответ: 10.

куда делось 50 и как получили 1/4?

Служба поддержки:

Числа разделили: 12,5 : 50 = 0,25.

    

↑Задание 13 № 99615 тип B13 Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно? Решение. Обозначим объем бака за 1. Тогда три насоса, работая вместе, заполнят бак за

минут. Ответ: 10.

↑Задание 14 № 245179 тип B14

Найдите наименьшее значение функции . Решение. Квадратный трехчлен с положительным старшим коэффициентом достигает наименьшего значения в точке , в нашем случае — в точке 3. Функция в этой точке определена и принимает значение . Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции.

Ответ: 2.

Начало формы

Задание С1 № 500917

Критерии оценивания выполнения задания	Баллы
Обоснованно получены верные ответы в п. а) и в п. б)	2
Обоснованно получен верный ответ в п. а), но обоснование отбора корней в п. б) не приведено, или задача в п. а) обоснованно сведена к исследованию простейших тригонометрических уравнений без предъявления верного ответа, а в п. б) приведён обоснованный отбор корней	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

а) Решите уравнение б) Найдите корни этого уравнения, принадлежащие промежутку

Решение.

а) Преобразуем уравнение: Значит, либо откуда либо откуда б) Отберем с помощью единичной окружности корни уравнения, принадлежащие заданному промежутку: Ответ: а) б)

Задание С2 № 484576

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

В правильной шестиугольной призме стороны основания которой равны 4, а боковые ребра равны 3, найдите расстояние от точкиВ до прямой .

Решение.

Так как ABCDEF правильный шестиугольник, то прямыеBE и CD параллельны, параллельны также прямые и , следовательно, прямые и параллельны. Расстояние от точки B до прямой , равно расстоянию между прямыми и .

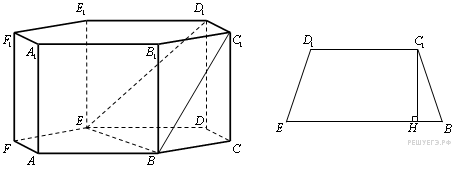
В трапеции : , , , ,

тогда . Ответ: .

Задание С3 № 485956

Критерии оценивания выполнения задания	Баллы
Получен верный обоснованный ответ	3
Оба неравенства решены верно, но ответ к системе отсутствует или неверный	2
Верно решено только одно из неравенств исходной системы	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	3

Решите систему неравенств

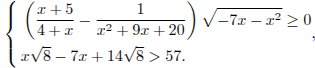
Решение. Решим первое неравенство.

1 случай: тогда или При этих выражение имеет смысл, поэтому числа и являются решениями неравенства. 2 случай: Решаем неравенство Получим: , или Решением первого неравенства системы является: или . Решим второе неравенство системы:

; ;

Учитывая, что , получаем:

.

Решением второго неравенства системы является: . , поэтому решением системы неравенств является: или .

Ответ: .

Задание С4 № 500215

Критерии оценивания выполнения задания	Баллы
Рассмотрены все возможные геометрические конфигурации и получен правильный ответ	3
Рассмотрена хотя бы одна возможная конфигурация, в которой получено правильное значение искомой величины	2
Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за арифметической ошибки	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	3

Продолжение биссектрисы неравнобедренного треугольника пересекает окружность, описанную около этого треугольника, в точке . Окружность, описанная около треугольника , пересекает прямую в точке , отличной от . Найдите радиус окружности, описанной около треугольника , если , , угол равен .

Решение.

Возможны два случая: 1) точка лежит между и (рис. 1); 2) точка лежит между и (рис. 2). Рассмотрим первый случай. , поэтому треугольники и равны. Значит, . Тогда искомый радиус равен . Рассмотрим второй случай. , поэтому треугольники и равны. Значит, . Тогда искомый радиус равен . Ответ: ; .

Задание С5 № 500477

Критерии оценивания выполнения задания	Баллы
Обоснованно получен правильный ответ	4
С помощью верного рассуждения получено множество значений а, отличающееся от искомого конечным числом точек	3
С помощью верного рассуждения получены все граничные точки искомого множества значений а	2
Верно получена хотя бы одна граничная точка искомого множества значений а	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	4

Найдите все значения а, при каждом из которых неравенство выполняется для всех .

Решение.

Рассмотрим функцию . Эта функция возрастает на промежутке и убывает па промежутке . Исходное неравенство имеет вид , значит, график функции на отрезке должен находиться в пределах горизонтальной полосы: Отрезок не должен лежать на участке монотонности функции , иначе приращение на отрезке длины 5 будет не меньше 25, поэтому её график не поместится в полосе ширины 20. Следовательно, , откуда . Наибольшее значение функции на отрезке достигается либо при , либо при . Наименьшее значение функции на отрезке достигается при . Получаем систему:

,

откуда . Ответ:

Задание С6 № 484659

Критерии оценивания ответа на задание С6	Баллы
Обоснованно получен верный ответ.	4
Решение не содержит логических пробелов, получен ответ, неверный только из-за вычислительной ошибки или описки.	3
Решение доведено до ответа, но содержит логические пробелы, вычислительные ошибки или описки. 2	2
Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок.	1
Все прочие случаи.	0
Максимальное количество баллов	4

Бесконечная десятичная дробь устроена следующим образом. Перед десятичной запятой стоит нуль. После запятой подряд выписаны члены возрастающей последовательности натуральных чисел В результате получилось рациональное число, которое выражается несократимой дробью, знаменатель которой меньше 100. Найдите наименьшее возможное значение .

Решение.

Очевидно, , причем , только если и , то есть если десятичная дробь начинается:

(четвертая цифра не 0).

Заметим, что таким образом начинается, например, число

Найдем число m и проверим, удовлетворяет ли оно условиям задачи. Для этого запишем сумму подробнее.

В каждой строчке — сумма геометрической прогрессии со знаменателем . Получаем:

.

Получается, что m — рациональное число, и оно представляется дробью со знаменателем 81, что меньше ста. Число m удовлетворяет условию задачи и для этого числа . Ответ: 3.