Задание с6 № 484653

Среди обыкновенных дробей с положительными знаменателями, расположенных между числами и , найдите такую, знаменатель которой минимален. Решение.

Так как

и ,

то достаточно найти правильную дробь с наименьшим знаменателем, лежащую между числами

и ,

а затем прибавить к ней число 2. Среди дробей со знаменателями 2, 3, 4, 5 и 6 нужных дробей нет, так как

, , , , , , , .

Для знаменателя 7 получаем , т. е.

.

Ответ: .

Вариант № 407

	Правильный ответ
1	77351	B1		4
2	26870	B2		13
3	27566	B3		25,5
4	26687	B4		420
5	26661	B5		35
6	27874	B6		70
7	77409	B7		36
8	500248	B8		3
9	245374	B9		45
10	320180	B10		0,52
11	27048	B11		5
12	28007	B12		60
13	26581	B13		10
14	77439	B14		6

↑ Задание 1 № 77351 тип B1

В доме, в котором живет Маша, 9 этажей и несколько подъездов. На каждом этаже находится по 4 квартиры. Маша живет в квартире № 130. В каком подъезде живет Маша? Решение. В доме, в котором живет Маша, на девяти этажах каждого подъезда 9   4 = 36 квартир. Разделим 130 на 36:

.

Значит, Маша живет в 4-м подъезде.

Ответ: 4.

↑ Задание 2 № 26870 тип B2

На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 15 июля. Ответ дайте в градусах Цельсия.

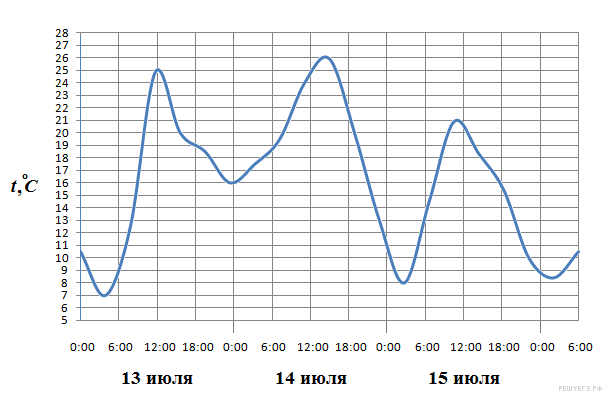
Решение. Из графика видно, что 15 июля наибольшая температура составляла 21 °C, а наименьшая 8 °C. Их разность составляет 13 °C. Ответ: 13.

Вопрос:Данные на графике и данные в решении не совпадают. Наибольшее по графику 27, а в решении написано 21, наименьшее по графику 7, а в решении написано 8

Ответ:Анализируем день 15 июля.

↑ Задание 3 № 27566 тип B3

Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10). Решение. Площадь треугольника равна разности площади квадрата со стороной 10 и трех прямоугольных треугольников, гипотенузы которых являются сторонами заданного треугольника. Поэтому

см². Ответ: 25,5.

↑ Задание 4 № 26687 тип B4

Для того, чтобы связать свитер, хозяйке нужно 400 граммов шерсти синего цвета. Можно купить синюю пряжу по цене 60 рублей за 50 г, а можно купить неокрашенную пряжу по цене 50 рублей за 50 г и окрасить ее. Один пакетик краски стоит 10 рублей и рассчитан на окраску 200 г пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка. Решение. Один моток пряжи весит 50 г, поэтому на свитер нужно 400:50 = 8 мотков. Рассмотрим различные варианты. Если покупать готовую пряжу синего цвета, то стоимость свитера будет 60   8 = 480 руб. На неокрашенную пряжу нужно потратить 50   8 = 400 руб. Но на окраску пряжи потребуется 2 пакетика по 10 руб., то есть еще 20 руб. Итого на свитер из самостоятельно окрашенной пряжи потратится 420 руб. Второй вариант дешевле, чем первый. Ответ: 420.

↑ Задание 5 № 26661 тип B5 Найдите корень уравнения . Решение. Возведем в квадрат: . Ответ: 35.

↑ Задание 6 № 27874 тип B6 Четырехугольник вписан в окружность. Угол равен , угол равен . Найдите угол . Ответ дайте в градусах. Решение. вписанный угол равен половине дуги, на которую он опирается, значит

Ответ: 70.

↑ Задание 7 № 77409 тип B7 Найдите значение выражения при . Решение. Выполним преобразования: . Ответ: 36.

↑ Задание 8 № 500248 тип B8

На рисунке изображён график дифференцируемой функции . На оси абсцисс отмечены девять точек: . Среди этих точек найдите все точки, в которых производная функции отрицательна. В ответе укажите количество найденных точек.

Решение. Производная функции отрицательна на тех интервалах, на которых функция убывает. Если сторону клетки принять за единицу, то функция убывает на интервалах (−4,4; −0,7) и (2,6;+∞). В них содержатся целые точки x₄, x₅, x₉. Их 3 штуки. Ответ: 3.

↑ Задание 9 № 245374 тип B9 Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Решение. 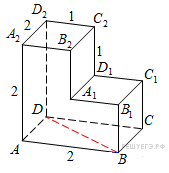— квадрат со стороной 2, а — его диагональ. Значит, треугольник — прямоугольный и равнобедренный, . Угол равен Ответ: 45.

↑ Задание 10 № 320180 тип B10

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. Решение. Джон промахнется, если схватит пристрелянный револьвер и промахнется из него, или если схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52. Ответ: 0,52.

Приведем другое решение. Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52. Правильный ответ: 0,52

↑ Задание 11 № 27048 тип B11

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см. Решение.Объем сосуда выражается через его высоту и сторону основания как . При увеличении стороны основания в 4 раза уровень воды уменьшится в 16 раз и будет равен 5 см.

Ответ: 5.

↑ Задание 12 № 28007 тип B12 Трактор тащит сани с силой кН, направленной под острым углом к горизонту. Мощность (в киловаттах) трактора при скорости м/с равна . При каком максимальном угле (в градусах) эта мощность будет не менее 75 кВт? Решение. Задача сводится к решению неравенства на интервале при заданных значениях силы кН и скорости м/ .Ответ: 60.

↑ Задание 13 № 26581 тип B13

Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч. Решение. Пусть км/ч – скорость велосипедиста на пути из B в A, тогда скорость велосипедиста на пути из A в B равна  км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:

Таким образом, скорость велосипедиста была равна 10 км/ч.

Ответ: 10.

↑ Задание 14 № 77439 тип B14 Найдите точку максимума функции . Решение. Найдем производную заданной функции: .

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума . Ответ: 6.

Начало формы