Задание с1 № 485942

Дано уравнение а) Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку

Решение.

а) По формуле приведения и формуле косинуса двойного угла: Тогда или Откуда или б) С помощью единичной окружности отберём корни на отрезке Это числа и (см. рис.). Ответ: а) б)

Задание с2 № 484562

В кубе найдите косинус угла между плоскостями и . Решение.

Пусть точка O — центр куба, а M — середина . , а MO — средняя линия треугольника , поэтому . Треугольник  — равносторонний, , следовательно, искомый угол равен углу .

Примем длины ребер куба за 1. Найдем стороны треугольника . Из треугольника , находим из треугольника находим

. ,

поскольку O — середина диагонали . Теперь применим к треугольнику теорему косинусов:

.

Ответ: .

Вопрос:Почему в условии не сказано о том, что дан единичный куб? или когда решаем подобные задачи, всегда берем сторону за 1?

Ответ:Вы можете взять куб с той стороной, с которой Вам будет удобнее, так как задача состоит в вычислении не длин, а их отношений (косинус угла характеризует отношение длин).

Вопрос:А ответ корень из 6 делить на 3 приняли бы?

Ответ:Да.

Задание С3 № 484600

Решите систему неравенств

Решение.

По смыслу задачи , , откуда .

При этих значениях переменной: , и .

Далее имеем:

.

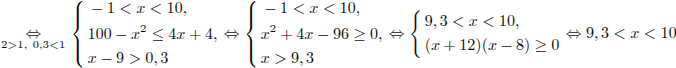Ответ: .

Задание с4 № 500900

Дан прямоугольник со сторонами: , . Прямая, проходящая через вершину M, касается окружности с центром радиуса 4 и пересекается с прямой в точке Найдите

Решение.

Пусть точка лежит между и (рис.1), — точка касания прямой с данной окружностью. Обозначим Из прямоугольного треугольника по теореме Пифагора находим

Прямоугольные треугольники и подобны, поэтому откуда

Если точка лежит на продолжении стороны за точку (рис.2), то, рассуждая аналогично, получим уравнение из которого Ответ: или .

Задание с5 № 500350

Найдите все значения , при которых уравнение на промежутке имеет ровно два корня.

Решение.

Рассмотрим функции и Исследуем на промежутке При все значения функции на промежутке неположительны, а все значения функции  — положительны, поэтому при уравнение не имеет решений на промежутке При функция возрастает на промежутке , Функция убывает на этом промежутке, поэтому уравнение всегда имеет ровно одно решение на промежутке , поскольку и На промежутке уравнение принимает вид Это уравнение сводится к уравнению Будем считать, что , поскольку случай был рассмотрен ранее. Дискриминант квадратного уравнения поэтому при это уравнение не имеет корней; при уравнение имеет единственный корень, равный ; при уравнение имеет два корня. Пусть уравнение имеет два корня, то есть Тогда оба корня меньше 4, поскольку при значения функции неположительны, а значения функции положительны. По теореме Виета сумма корней равна 3, а произведение равно Значит, больший корень всегда принадлежит промежутку , а меньший принадлежит этому промежутку тогда и только тогда, когда . Таким образом, уравнение имеет следующее количество корней на промежутке : 1) Нет корней при 2) Один корень при 3) Два корня при и 4) Три корня при Ответ: ;