Задание с6 № 484657

Произведение всех делителей натурального числа N оканчивается на 399 нулей. На сколько нулей может оканчиваться число N?

Решение.

Разложим N на простые множители:

,

где p — наибольший простой множитель и Если запись числа N оканчивается n нулями, то или или, наоборот, . Оценим количество делителей k числа N:

,

при этом k делится на . 1 случай. Если k — четное, то все делители разбиваются на пар вида так, что произведение делителей в каждой паре равно N. Поэтому произведение всех делителей равно . 2 случай. Если k — нечетное, то делителей разбиваются на пары указанного вида, и есть еще один делитель — . И в этом случае тоже произведение всех делителей: . Значит, для любого N произведение всех делителей оканчивается нулями, следовательно, . При этом , откуда следует, что n — делитель числа 798, и . Выпишем все такие n: 1,2,3,6,7. Из равенства также следует, что 798 делится на . Поэтому возможно только и . Для каждого из этих n подберем настоящее N. Ограничимся простыми множителями 2 и 5. Значит, нужно подобрать только и . 1. . 2. . 3. , ; ; . Таким образом, для найдены ( и даже не все) N, оканчивающиеся n нулями, произведение делителей которых оканчивается 399 нулями. Ответ: 1, 2, 6.

Результаты Вариант № 406

№ п/п	Номер	Тип		Правильный ответ
1	26627	B1		34
2	27521	B2		2
3	55603	B3		42
4	26689	B4		16470
5	77381	B5		2
6	27868	B6		100
7	26787	B7		7
8	119976	B8		20
9	911	B9		17
10	320189	B10		0,498
11	27158	B11		30
12	42869	B12		3
13	99599	B13		80
14	26704	B14		11

↑ Задание 1 № 26627 тип B1

Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей? Решение. С учетом наценки учебник будет стоить 170 + 0,2   170 = 204 рубля. Разделим 7000 на 204:

.Значит, можно будет купить 34 учебника.

Ответ: 34.

↑ Задание 2 № 27521 тип B2

На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура превышала 20 градусов Цельсия.

Решение. Из диаграммы видно, что было 2 месяца, когда среднемесячная температура превышала 20 градусов Цельсия (см. рисунок).

Ответ: 2.

↑ Задание 3 № 55603 тип B3

Площадь круга равна . Найдите длину его окружности.

Решение. Пусть радиус окружности равен R, тогда площадь круга определяется формулой S = πR², длина окружности определяется формулой l = 2πR. Поэтому

, , значит,

Ответ: 42.

↑ Задание 4 № 26689 тип B4

При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 9 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1 600 рублей, щебень стоит 780 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант? Решение. Рассмотрим два варианта. Стоимость каменного фундамента складывается из стоимости камня 9   1600 = 14 400 руб., а также стоимости цемента 9   230 = 2070 руб. и составляет 2070 + 14 400 = 16 470 руб. Стоимость бетонного фундамента складывается из стоимости цемента 50   230 = 11 500 руб., а также стоимости щебня 7   780 = 5460 руб. и составляет 5460 + 11 500 = 16 960 руб. Стоимость самого дешевого варианта составляет 16 470 рублей.

Ответ: 16 470.

↑ Задание 5 № 77381 тип B5

Решите уравнение . Решение. Заметим, что и используем формулу Имеем:

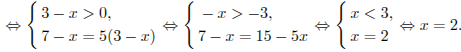Ответ: 2.

↑ Задание 6 № 27868 тип B6

Точки , , , расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как . Найдите больший угол треугольника . Ответ дайте в градусах. Решение. пусть меньшая часть окружности равна тогда

Вписанный угол равен половине дуги, на которую он опирается, значит,

Ответ: 100.

Задание 7 № 26787 тип B7

Найдите , если . Решение. Выполним преобразования:

.

Ответ: 7.

↑ Задание 8 № 119976 тип B8

Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с. Решение. Найдем закон изменения скорости:

м/с. Тогда находим: м/с.

Ответ: 20.

↑ Задание 9 № 911 тип B9 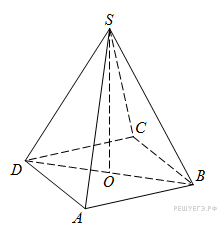В правильной четырехугольной пирамиде точка – центр основания, – вершина, , . Найдите боковое ребро . Решение. В правильной пирамиде вершина проецируется в центр основания, следовательно является высотой пирамиды. тогда по теореме Пифагора

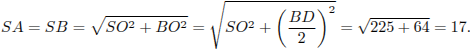
Ответ: 17.

↑ Задание 10 № 320189 тип B10

В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных. Решение. Из 5000 тысяч новорожденных 5000 − 2512 = 2488 девочек. Поэтому частота рождения девочек равна

Ответ: 0,498.

↑ Задание 11 № 27158 тип B11

Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов. Решение. Площадь поверхности креста равна площади поверхности 6-ти кубов, у которых отсутствует одна из шести сторон. Получаем, что площадь поверхности: . Ответ: 30.

↑ Задание 12 № 42869 тип B12

Уравнение процесса, в котором участвовал газ, записывается в виде , где  (Па) — давление в газе,  — объeм газа в кубических метрах,  — положительная константа. При каком наименьшем значении константы увеличение в 3 раза объeма газа, участвующего в этом процессе, приводит к уменьшению давления не менее, чем в 27 раз? Решение. Пусть и – начальные, а и – конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства , причем : .

Значит, наименьшее значение константы равно 3. Ответ: 3.

↑ Задание 13 № 99599 тип B13

Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. Решение. К моменту первого обгона мотоциклист за 10 минут проехал столько же, сколько велосипедист за 40 минут, следовательно, его скорость в 4 раза больше. Поэтому, если скорость велосипедиста принять за x км/час, то скорость мотоциклиста будет равна 4x, а скорость их сближения — 3x км/час. C другой стороны, второй раз мотоциклист догнал велосипедиста за 30 минут, за это время он проехал на 30 км больше. Следовательно, скорость их сближения составлят 60 км/час. Итак, 3х = 60 км/час, откуда скорость велосипедиста равна 20 км/час, а скорость мотоциклиста равна 80 км/час.

↑ Задание 14 № 26704 тип B14 Найдите наибольшее значение функции на отрезке . Решение. Найдем производную заданной функции:

Найденная производная неотрицательна на заданном отрезке, заданная функция возрастает на нем, поэтому наибольшим значением функции на отрезке является

Ответ: 11.

Начало формы