Задание с1 № 484542
Критерии оценивания выполнения задания |
Баллы |
Система решена верно |
2 |
Тригонометрическое уравнение получено и решено верно, система решена неверно. |
1 |
Все прочие случаи |
0 |
Максимальный балл |
2 |
Решите
систему уравнений
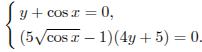
Решение.
Из второго уравнения получаем:
или
.
Если
,
то из первого уравнения
.
Уравнение не имеет решений. Если
то
,
и из первого уравнения получаем:
.
Ответ:
.
Ваша оценка (баллов):
Вопрос: а можно написать в ответе:+-arccos1/25+2пn,-1/25.??
Ответ:Можно.
Вопрос: Почему при y=-5/4 нет решений?
Ответ:При y=-5/4, cos(x)>1, чего не может быть.
Задание с2 № 500193
Точка — середина ребра куба . Найдите площадь сечения куба плоскостью , если ребра куба равны 2.
Решение.
Прямая пересекает прямую в точке . Прямая пересекает ребро в его середине — точке . — сечение куба плоскостью . В равнобедренном треугольнике , и высота . Поскольку — средняя линия треугольника , получаем:
Ответ: 4,5.
Задание с3 № 484595
Решите
неравенство
.
Решение.
Решение будем искать при условиях:
откуда
.
Рассмотрим исходное неравенство
при
,
тогда
,
откуда
,
то есть
.
Рассмотрим исходное неравенство
при
,
тогда
,
откуда
,
то есть
.
Ответ:
.
Задание с4 № 500015
Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке М. Найдите радиус окружности, вписанной в треугольник ВМС.
Решение.
В любой трапеции отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований трапеции, а средняя линия — полусумме оснований трапеции. В нашем случае полуразность оснований равна 5, а полусумма оснований равна 25, поэтому основания трапеции равны 20 и 30. Предположим что (рис. 1). Стороны BС и АD треугольников МВС и MAD параллельны, поэтому эти треугольники подобны с коэффициентом Значит,
, .
Заметим, что , поэтому треугольник МВС — прямоугольный с гипотенузой BС. Радиус его вписанной окружности равен: . Пусть теперь , (рис. 2). Аналогично предыдущему случаю можно показать, что радиус вписанной окружности треугольника MAD равен 6. Треугольник MAD и МВС подобны с коэффициентом Значит, радиус вписанной окружности треугольника МВС равен .
Ответ: 4; 6.
Задание с5 № 500390
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите все значения , при каждом из которых уравнение имеет более двух корней.
Решение.
Рассмотрим
функции
и
.
Исследуем уравнение
.
На промежутке
функция
возрастает.
Функция
убывает
на этом промежутке, поэтому уравнение
имеет
не более одного решения на промежутке
,
причем решение будет существовать тогда
и только тогда, когда,
,
то есть при
.
При
уравнение
принимает
вид
.
При
левая
часть этого уравнения отрицательна,
следовательно, решений нет. При
это
уравнение сводится к квадратному
уравнению
дискриминант
которого
,
поэтому при
это
уравнение не имеет корней; при
уравнение
имеет единственный корень, равный
;
при
уравнение
имеет два корня.
Пусть уравнение
имеет два корня,
и .
Тогда меньший корень всегда меньше , а больший корень не превосходит , если , то есть при . По теореме Виета:
, ,
поэтому знаки корней и зависят от знаков выражений и . Значит, при оба корня отрицательны, при один из корней отрицательный, а другой неотрицательный, при оба корня неотрицательны. Таким образом, при уравнение не имеет корней при и , имеет один корень при и , имеет два корня при . Таким образом, уравнение имеет следующее количество корней: — нет корней при ; — один корень при и ; — два корня при и ; — три корня при . Ответ: .
Ваша оценка (баллов):
Вопрос:Аналитический метод хорош, но несколько сложен. Проще графическое решение: найти касательную к уравнению с корнем и получим крайнее значение параметра. Другое же значение параметра будет видно из точки пересечения графиков уравнений.