Задание с5 № 484635

При каких значениях параметра а система имеет четыре решения?

Решение.

Полагая , , перепишем систему в виде

Заметим, теперь что если пара является решением системы, то и пара  — также решение этой системы. Следовательно, если  — решение системы такое, что и , , то система будет иметь восемь решений. Таким образом, исходная система будет иметь четыре решения в следующих двух случаях: , или . А тогда, если ; то . Если же или , то . Ответ: , .

Задание с6 № 484662

Каждое из чисел 5, 6, . . ., 9 умножают на каждое из чисел 12, 13, . . ., 17 и перед каждым произвольным образом ставят знак плюс или минус, после чего все 30 полученных результатов складывают. Какую наименьшую по модулю сумму и какую наибольшую сумму можно получить в итоге?

Решение.

1. Если все произведения взяты со знаком плюс, то их сумма наибольшая и она равна

.

2. Так как сумма нечетная, число нечетных слагаемых в ней — нечетно, причем это свойство суммы не меняется при изменении знака любого ее слагаемого. Поэтому любая из получающихся сумм будет нечетной, а значит, не будет равна 0. 3. Значение 1 сумма принимает, например, при такой расстановке знаков у произведения, которая получится при раскрытии следующих скобок

.

Ответ: 1 и 3045.

Конец формы

Результаты Вариант № 405

№ п/п	Номер	Тип		Правильный ответ
1	26621	B1		6
2	27516	B2		-2
3	27578	B3		6
4	319558	B4		1
5	39007	B5		23
6	27415	B6		4
7	68191	B7		0
8	27496	B8		5
9	284361	B9		2
10	282853	B10		0,14
11	27088	B11		3
12	27979	B12		5
13	26579	B13		52
14	77482	B14		0

↑ Задание 1 № 26621 тип B1

Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей? Решение. С учетом наценки горшок станет стоить 120 + 0,2   120 = 144 рубля. Разделим 1000 на 144:

. Значит, можно будет купить 6 горшков.

Ответ: 6.

↑ Задание 2 № 27516 тип B2

На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.

Решение. Из диаграммы видно, что наименьшая среднемесячная температура во второй половине года составляла −2 °C (см. рисунок).

Ответ: −2.

↑ Задание 3 № 27578 тип B3

Найдите площадь параллелограмма, изображенного на рисунке. Решение. Площадь параллелограмма равна произведению основания на высоту: .

Ответ: 6.

↑ Задание 4 № 319558 тип B4

Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены и оценок функциональности , качества и дизайна . Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

Модель печи	Средняя цена	Функциональность	Качество	Дизайн
А	1900	1	1	1
Б	5900	4	1	2
В	3800	0	0	1
Г	4100	2	0	4

Решение. Рассмотрим все варианты. Модель А: Модель Б: Модель В: Модель Г: Таким образом, наивысший рейтинг имеет модель А. Он равен 1.

Ответ: 1.

↑ Задание 5 № 39007 тип B5 Найдите корень уравнения .

Решение. Возведем обе части уравнения в третью степень:

Ответ: 23.

↑ Задание 6 № 27415 тип B6

В треугольнике угол равен 90°, тангенс внешнего угла при вершине равен –0,5, . Найдите . Решение. . Ответ: 4.

↑ Задание 7 № 68191 тип B7 Найдите , если .

Решение. Подставим аргументы в формулу, задающую функцию:

.

Следовательно, . Ответ: 0.

↑ Задание 8 № 27496 тип B8

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

Решение. Точки экстремума соответствуют точкам смены знака производной — изображенным на графике нулем производной. Производная обращается в нуль в точках −6, −2, 2, 6, 9. На отрезке [−10; 10] функция имеет 5 точек экстремума. Ответ: 5.

↑ Задание 9 № 284361 тип B9

Площадь боковой поверхности цилиндра равна , а диаметр основания — 1. Найдите высоту цилиндра. Решение. Площадь боковой поверхности цилиндра находится по формуле: , значит, . Правильный ответ: 2

↑ Задание 10 № 282853 тип B10 В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение. Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна

Ответ: 0,14.

Ваш ответ: нет ответа. Правильный ответ: 0,14

Вопрос: Количество исходов равно 6, вы забыли то, что комбинация 4-4 повторяется дважды.

Слу жба поддержки:Решение верно. Комбинация 4+4 означает, что на обоих кубиках выпали четверки, это один случай.

Вопрос: А можно было решать таким способом: мы учитываем повторение одинаковых комбинаций, и поэтому представляем решение как отношение 3/21 ( 3 - случая выпадение 8, 21 - всевозможное выпадение ) Просто ответ как бы сходится, но вот можно было так решать я не знаю.Буду признателен за помощь!

Служба поддержки:

Ваш ответ отличается от правильного.

Тем, что рассуждение неправильное и ответ неверный. В задаче благоприятных случаев 5, а всего их 36.

Вопрос: Почему не рассматривались такие варианты выпадения кубика как: 1+7 и 7+1?

Служба поддержки:У кубиков по 6 граней.

↑ Задание 11 № 27088 тип B11

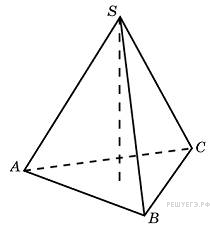Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен . Решение. Объем пирамиды равен ,где  — площадь основания, а  — высота пирамиды. Найдем площадь равностороннего треугольника, лежащего в основании:

.Тогда высота пирамиды равна

Ответ: 3.

↑ Задание 12 № 27979 тип B12

К источнику с ЭДС В и внутренним сопротивлением Ом, хотят подключить нагрузку с сопротивлением Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даeтся формулой . При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 50 В? Ответ выразите в Омах. Решение. Задача сводится к решению неравенства В при известных значениях внутреннего сопротивления Ом, ЭДС В:

Ом.

Ответ: 5.

↑ Задание 13 № 26579 тип B13

Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути – со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч. Решение. Пусть км/ч – скорость первого автомобиля, тогда скорость второго автомобиля на первой половине пути равна  км/ч. Примем расстояние между пунктами за 2. Автомобили были в пути одно и то же время, отсюда имеем:

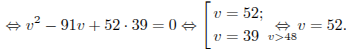
Таким образом, скорость первого автомобиля была равна 52 км/ч.

Ответ: 52.

↑ Задание 14 № 77482 тип B14 Найдите наименьшее значение функции на отрезке . Решение. Найдем производную заданной функции . Найдем нули производной:

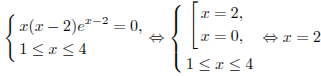
Определим знаки производной функции и изобразим на рисунке поведение функции:

В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение: .

Ответ: 0.

Начало формы