Проверка части с

Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь указанными критериями.

Начало формы

Задание с1 № 484557

Критерии оценивания выполнения задания	Баллы
Обоснованно полученные верные ответы	2
Обоснованно получен верный ответ, но обоснование отбора корней не приведено или задача сведена к исследованию простейших тригонометрических уравнений без предъявления верного ответа	1
Решение не соответствует ни одному из критериев	0
Максимальный балл	2

Решите уравнение .

Решение.

Левая часть уравнения имеет смысл при . Если , то . Если , то , откуда . Учитывая, что , из уравнения получаем:

.

Ответ: , .

Ваша оценка (баллов):

    Обсудить ВКонтакте    Сообщить об ошибке

Задание с2 № 484560

Критерии оценивания выполнения задания	Баллы
Обоснованно получен верный ответ	2
Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

В правильной треугольной SABC пирамиде с основанием ABC известны ребра . Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC.

Решение.

Пусть N — середина ребра BC, а M — середина AS. Прямая AS проецируется на плоскость основания в прямую AN. Поэтому проекция точки M — точка  — лежит на отрезке AN. Значит, прямая AN является проекцией прямой AM, следовательно, угол  — искомый. Поскольку , где O — центр основания,  — средняя линяя треугольника SAO.

Тогда

Кроме того,

Из прямоугольного треугольника находим:

.

Ответ: .

Ваша оценка (баллов):

    Обсудить ВКонтакте    Сообщить об ошибке

Задание с3 № 500589

Критерии оценивания выполнения задания	Баллы
Получен верный обоснованный ответ	3
Оба неравенства решены верно, но ответ к системе отсутствует или неверный	2
Верно решено только одно из неравенств	1
Не решено верно ни одно из неравенств	0
Максимальный балл	3

Решите систему неравенств

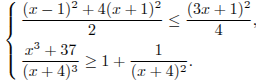
Решение.

Решим первое неравенство:

.

Проверим, удовлетворяет ли число −3 второму неравенству:

,

что верно. Следовательно, число −3 удовлетворяет второму неравенству. Ответ: −3

Задание с4 № 500876

Дан прямоугольник со сторонами: , . Прямая, проходящая через вершину M, касается окружности с центром радиуса 4 и пересекается с прямой в точке Найдите

Решение.

Пусть точка лежит между и (рис.1), — точка касания прямой с данной окружностью. Обозначим

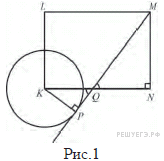
Из прямоугольного треугольника по теореме Пифагора находим

Прямоугольные треугольники и подобны, поэтому откуда

Если точка лежит на продолжении стороны за точку (рис.2), то, рассуждая аналогично, получим уравнение из которого Ответ: или .