Результаты Вариант № 403

№ п/п	Номер	Тип	Правильный ответ
1	26622	B1	10
2	27523	B2	4
3	500243	B3	18
4	26673	B4	700
5	38675	B5	7
6	27807	B6	125
7	85983	B7	13
8	123715	B8	3
9	284353	B9	1
10	320200	B10	0,978
11	27184	B11	2
12	27998	B12	30
13	99567	B13	15
14	77459	B14	4

↑ Задание 1 № 26622 тип B1

В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели? Решение. За 4 недели в офисе расходуется 1200   4 = 4800 листов бумаги. Разделим 4800 на 500:

.

Значит, можно будет купить 10 пачек. Ответ: 10.

↑ Задание 2 № 27523 тип B2

На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода не выпадало осадков.

Решение. Из графика видно, что 4 дня из данного периода (5, 8, 9, 12 февраля) не выпадало осадков (см. рисунок).

Ответ: 4.

↑ Задание 3 № 500243 тип B3

Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах. Решение. Площадь трапеции равна произведению полусуммы оснований на высоту:

 см². Ответ: 18

↑ Задание 4 № 26673 тип B4

Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.

Тарифный план	Абонентская плата	Плата за трафик
План «0»	Нет	2,5 руб. за 1 Мб
План «500»	550 руб. за 500 Мб трафика в месяц	2 руб. за 1 Мб сверх 500 Мб
План «800»	700 руб. за 800 Мб трафика в месяц	1,5 руб. за 1 Мб сверх 800 Мб

Пользователь предполагает, что его трафик составит 600 Мб в месяц и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 600 Мб? Решение. Рассмотрим все варианты. По Плану «0» пользователь потратит 2,5   600 = 1500 руб. в месяц за 600 Мб трафика. По плану «500» он потратит 550 руб. абонентской платы за 500 Мб и 2   100 = 200 руб. сверх того. Поэтому полная плата в месяц составит 550 + 200 = 750 руб. По плану «800» пользователь потратит в месяц за 600 Мб трафика 700 руб. Наиболее выгодный вариант составляет 700 руб.

Ответ: 700.

↑ Задание 5 № 38675 тип B5 Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.

Решение. Сумма корней уравнения равна 15, а их произведение равно 56. Следовательно, это числа 7 и 8. Меньший из них равен 7. Ответ: 7.

↑ Задание 6 № 27807 тип B6

Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах. Решение. сумма углов, прилежащих к одной стороне параллелограмма равна , а их разница равна .

. Ответ: 125.

↑ Задание 7 № 85983 тип B7 Найдите значение выражения при .

Решение. Поскольку , имеем:

. Ответ: 13.

Приведем другое решение. По условию , поэтому . Тогда имеем:

↑ Задание 8 № 123715 тип B8 Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 4 м/с?

Решение. Найдем закон изменения скорости: .

Чтобы найти, в какой момент времени t скорость была равна 4 м/с, решим уравнение: с.

Следовательно, скорость точки была равна 4 м/с на третьей секунде движения.

Ответ: 3.

↑ Задание 9 № 284353 тип B9

В правильной треугольной пирамиде точка  — середина ребра ,  — вершина. Известно, что , а площадь боковой поверхности равна 3. Найдите длину отрезка . Решение. Площадь боковой поверхности правильной пирамиды равна произведению апофемы на полупериметр основания. Поэтому

Ответ: 1.

↑ Задание 10 № 320200 тип B10 На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных. Решение. Пусть завод произвел тарелок. В продажу поступят все качественные тарелки и 20% невыявленных дефектных тарелок: тарелок. Поскольку качественных из них , вероятность купить качественную тарелку равна

Ответ: 0,978.

↑ Задание 11 № 27184 тип B11

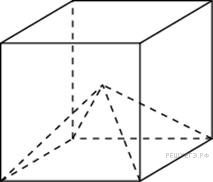Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба. Решение. Объем пирамиды равен . Ответ: 2.

↑ Задание 12 № 27998 тип B12

Мяч бросили под углом к плоской горизонтальной поверхности земли. Время полeта мяча (в секундах) определяется по формуле . При каком наименьшем значении угла (в градусах) время полeта будет не меньше 3 секунд, если мяч бросают с начальной скоростью м/с? Считайте, что ускорение свободного падения м/с . Решение. Задача сводится к решению неравенства на интервале при заданных значениях начальной скорости и ускорения свободного падения:

. Ответ: 30.

↑ Задание 13 № 99567 тип B13 Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки? Решение. Стоимость четырех рубашек составляет 92% стоимости куртки. Значит, стоимость одной рубашки составляет 23% стоимости куртки. Поэтому стоимость пяти рубашек составляет 115% стоимости куртки. Это превышает стоимость куртки на 15%. Ответ: 15.

↑ Задание 14 № 77459 тип B14 Найдите точку минимума функции . Решение. Найдем производную заданной функции: .

Найдем нули производной: .

Определим знаки производной функции и изобразим на рисунке поведение функции:

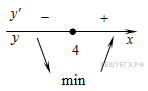Искомая точка минимума . Ответ: 4.

Начало формы

Задание С1 № 500012

а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку .

Решение.

Решим уравнение:

Отберём корни, принадлежащие отрезку . Это числа (см. рис.): .

Ответ: A) . Б) ; ; .

    

Задание С2 № 500213

На ребре куба отмечена точка так, что . Найдите угол между прямыми и .

Решение.

Примем ребро куба за единицу. Тогда . Поскольку , получаем: и . Проведем через точку прямую, параллельную . Она пересекает ребро в точке , причем треугольники и равны. Искомый угол равен углу (или смежному с ним). В прямоугольном треугольнике с прямым углом

В прямоугольном треугольнике с прямым углом

В треугольнике

откуда

, тогда

Ответ может быть представлен и в другом виде: или Ответ: .

Задание С3 № 485950

Решите систему неравенств:

Решение.

Рассмотрим второе неравенство. Оно имеет смысл при т. е. при Пусть Тогда неравенство принимает вид откуда . Имеем:

Подставим в первое неравенство найденные значения : 1. При : 2. При : 3. При : Неравенству удовлетворяют значения и

Ответ: ;

Задание С4 № 500015

Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке М. Найдите радиус окружности, вписанной в треугольник ВМС.

Решение.

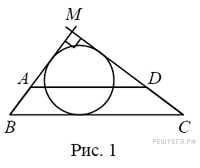В любой трапеции отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований трапеции, а средняя линия — полусумме оснований трапеции. В нашем случае полуразность оснований равна 5, а полусумма оснований равна 25, поэтому основания трапеции равны 20 и 30. Предположим что (рис. 1). Стороны BС и АD треугольников МВС и MAD параллельны, поэтому эти треугольники подобны с коэффициентом Значит,

, .

Заметим, что , поэтому треугольник МВС — прямоугольный с гипотенузой BС. Радиус его вписанной окружности равен: . Пусть теперь , (рис. 2). Аналогично предыдущему случаю можно показать, что радиус вписанной окружности треугольника MAD равен 6. Треугольник MAD и МВС подобны с коэффициентом Значит, радиус вписанной окружности треугольника МВС равен .

Ответ: 4; 6.

Задание С5 № 500135

Найдите все значения а. при каждом из которых уравнение

на промежутке имеет более двух корней.

Решение.

Рассмотрим функции и . Исследуем уравнение на промежутке . При все значения функции на промежутке отрицательны, а все значения функции  — неотрицательны, поэтому при уравнение не имеет решений на промежутке . При функция возрастает. Функция убывает на промежутке , поэтому уравнение имеет не более одного решения на промежутке , причем решение будет существовать тогда и только тогда, когда, , откуда получаем , то есть . На промежутке уравнение принимает вид . Это уравнение сводится к уравнению . Будем считать, что , поскольку случай был рассмотрен ранее. Дискриминант квадратного уравнения , поэтому при это уравнение не имеет корней; при уравнение имеет единственный корень, равный 2; при уравнение имеет два корня. Если уравнение имеет два корня и , то есть , то больший корень , поэтому он принадлежит промежутку . Меньший корень принадлежит промежутку тогда и только тогда, когда

то есть

Таким образом, уравнение имеет следующее количество корней на промежутке : - нет корней при ; - один корень при и ; - два корня при и ; - три корня при . Ответ: .

Задание С6 № 500197

Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары групп находят модуль разности найденных сумм и полученные 6 чисел складывают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Каково наименьшее возможное значение полученного результата?

Решение.

Обозначим суммы чисел в группах , , , а указанную в условии сумму модулей их попарных разностей через . Можно считать, что . а) Чтобы число равнялось 0, необходимо, чтобы каждая из разностей равнялась 0, то есть . Сумма всех двенадцати чисел . С другой стороны, она равна , но 78 не делится на 4. Значит, . б) Чтобы число равнялось 1, необходимо, чтобы все, кроме одной, разности равнялись 0. Значит, , но в этом случае каждая из сумм , не равна хотя бы одной из сумм , поэтому хотя бы три разности не равны 0 и число не меньше 3. Значит, . в) Выразим число явно через , , , :

В предыдущих пунктах было показано, что . Если , то или . В этом случае сумма всех двенадцати чисел равна или , то есть нечётна, что неверно. Для следующего разбиения чисел на группы: ; ; ; — число равно 4. Ответ: а) нет; б) нет; в) 4.