
- •Результаты Вариант № 275
- •Результаты Вариант № 276
- •Результаты Вариант № 277
- •Задание 4 № 316049 тип b4
- •Задание с1 № 500131
- •Задание с2 № 500588
- •Задание с3 № 484579
- •Задание с4 № 485990
- •Задание с5 № 484630
- •Задание с6 № 500412
- •Результаты Вариант № 278
- •Результаты Вариант № 399
- •Решения
- •Проверка части с
- •Результаты Вариант № 400
- •Результаты Вариант № 401
- •Проверка части с
- •Результаты Вариант № 402
- •Результаты Вариант № 403
- •Результаты Вариант № 404
- •Проверка части с
- •Задание с1 № 484557
- •Задание с2 № 484560
- •Задание с3 № 500589
- •Задание с4 № 500876
- •Задание с5 № 484635
- •Задание с6 № 484662
- •Результаты Вариант № 405
- •Задание с1 № 484542
- •Задание с2 № 500193
- •Задание с3 № 484595
- •Задание с4 № 500015
- •Задание с5 № 500390
- •Задание с6 № 484657
- •Результаты Вариант № 406
- •Задание с1 № 485942
- •Задание с2 № 484562
- •Задание с4 № 500900
- •Задание с5 № 500350
- •Задание с6 № 484653
- •Вариант № 407
- •Задание с1 № 485996
- •Задание с2 № 484574
- •Задание с3 № 485951
- •Задание с4 № 485949
- •Задание с5 № 484644
- •Задание с6 № 500017
- •Вариант № 408
- •Задание с1 № 485973
- •Задание с2 № 484560
- •Задание с3 № 485969
- •Задание с4 № 500003
- •Задание с5 № 500471
- •Задание с6 № 484656
- •Вариант № 409
- •Задание с1 № 484553
- •Задание с2 № 500024
- •Задание с3 № 485944
- •Задание с4 № 484616
- •Задание с5 № 500016
- •Задание с6 № 500005
- •Вариант № 410
- •Задание с1 № 485977
- •Задание с2 № 486000
- •Задание с3 № 500020
- •Задание с4 № 485945
- •Задание с5 № 484642
- •Задание с6 № 500820
- •Результаты Вариант № 411
- •Задание с1 № 484550
- •Задание с2 № 484577
- •Задание с3 № 484604
- •Задание с4 № 500430
- •Задание с5 № 500196
- •Задание с6 № 484655
- •Результаты Вариант № 412
- •Задание с1 № 485964
- •Задание с2 № 500013
- •Задание с3 № 500368Решить систему неравенств
- •Задание с4 № 500369
- •Задание с5 № 484645
- •Задание с6 № 484666
- •Результаты Вариант № 413
- •Задание с1 № 500638 а) Решите уравнение . Б) Найдите все корни этого уравнения, принадлежащие промежутку .
- •Задание с2 № 500387
- •Задание с3 № 500449
- •Задание с4 № 500349
- •Задание с5 № 484648
- •Задание с6 № 500452
- •Вариант № 1939 447
- •Задание с1 № 484542
- •Задание с2 № 485981
- •Задание с3 № 484598
- •Задание с4 № 484615
- •Задание с5 № 500965
- •Задание с6 № 484655
- •Результаты Вариант № 14
- •Проверка части с
- •Результаты варианта 12
- •Результаты варианта 4 и 12
- •Проверка части с
- •Задание с1 № 500427
- •Задание с2 № 484571
- •Задание с3 № 500388
- •Задание с4 № 484610
- •Задание с5 № 484633
- •Задание с6 № 485960
- •Вариант № 1940591
- •Задание с1 № 485977
- •Задание с2 № 484559
- •Задание с3 № 500449
- •Задание с4 № 500410
- •Задание с5 № 484647
- •Задание с6 № 500966
- •Вариант № 1941093
- •Задание с1 № 500638
- •Задание с2 № 485955
- •Задание с3 № 500409
- •Задание с4 № 484613
- •Задание с5 № 484644
- •Задание с6 № 484654
- •Вариант № 1941368
- •Задание с1 № 484553 Решите уравнение .
- •Задание с2 № 484559
- •Задание с3 № 500368
- •Задание с4 № 500015
- •Задание с5 № 484633
- •Задание с6 № 484655
Результаты Вариант № 402
№ п/п |
Номер |
Тип |
|
Правильный ответ |
1 |
314867 |
B1 |
|
211,2 |
2 |
26868 |
B2 |
|
-10 |
3 |
500030 |
B3 |
|
9 |
4 |
26677 |
B4 |
|
311 |
5 |
26656 |
B5 |
|
3 |
6 |
282852 |
B6 |
|
94 |
7 |
26764 |
B7 |
|
-12 |
8 |
317539 |
B8 |
|
5 |
9 |
914 |
B9 |
|
16 |
10 |
320172 |
B10 |
|
0,52 |
11 |
25601 |
B11 |
|
110 |
12 |
43145 |
B12 |
|
7 |
13 |
111867 |
B13 |
|
8 |
14 |
77490 |
B14 |
|
1 |
↑ Задание 1 № 314867 тип B1 В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб. м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях. Решение. Расход воды составил 114 − 103 = 11 куб. м. Поэтому Алексей должен заплатить 11 19,2 = 211,2 руб.
Ответ: 211,2.
↑ Задание 2 № 26868 тип B2
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 22 января. Ответ дайте в градусах Цельсия.
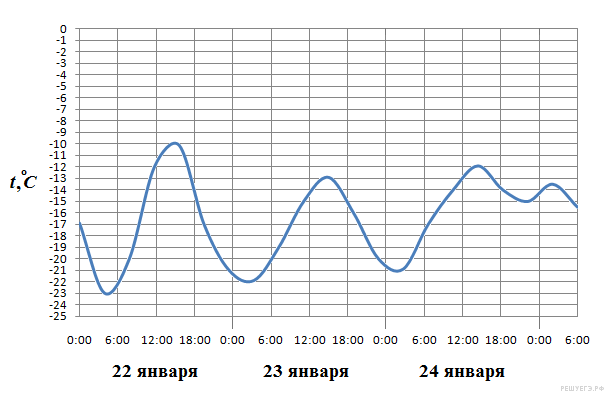 Решение.
Из
графика видно, что наибольшая температура
воздуха 22 января составляла −10 °C
(см. рисунок).
Решение.
Из
графика видно, что наибольшая температура
воздуха 22 января составляла −10 °C
(см. рисунок).
Ответ: −10.
↑ Задание 3 № 500030 тип B3
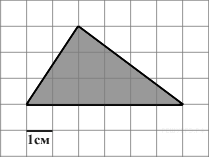 Найдите
площадь треугольника, изображённого
на клетчатой бумаге с размером клетки
1 см х 1 см (см. рис.). Ответ
дайте в квадратных сантиметрах.
Решение.
Найдите
площадь треугольника, изображённого
на клетчатой бумаге с размером клетки
1 см х 1 см (см. рис.). Ответ
дайте в квадратных сантиметрах.
Решение.
 Площадь
треугольника равна половине произведения
высоты на основание. Высота равна 3 см,
основание равно 6 см, поэтому площадь
изображённого треугольника равна 9
квадратным сантиметрам.
Площадь
треугольника равна половине произведения
высоты на основание. Высота равна 3 см,
основание равно 6 см, поэтому площадь
изображённого треугольника равна 9
квадратным сантиметрам.
Ответ: 9.
↑ Задание 4 № 26677 тип B4 Телефонная компания предоставляет на выбор три тарифных плана.
Тарифный план |
Абонентская плата |
Плата за 1 минуту разговора |
Повременный |
135 руб. в месяц |
0,3 руб. |
Комбинированный |
255 руб. за 450 мин. в месяц |
0,28 руб. за 1 мин. сверх 450 мин. в месяц |
Безлимитный |
380 руб. в месяц |
|
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 650 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 650 минут? Ответ дайте в рублях. Решение. Рассмотрим три случая. На тарифном плане «Повременный» ежемесячная плата будет складываться из абонентской 135 руб. и платы за 650 мин. 650 0,3 = 195 руб. и будет составлять 195 + 135 = 330 руб. На тарифном плане «Комбинированный» ежемесячная плата будет складываться из абонентской 255 руб. и платы за 200 мин. сверх тарифа 200 0,28 = 56 руб. и будет составлять 255 + 56 = 311 руб. На тарифном плане «Безлимитный» ежемесячная плата будет равна 380 рублям. Стоимость самого дешевого варианта составляет 311 рублей. Ответ: 311.
↑ Задание 5 № 26656 тип B5 Найдите корень уравнения . Решение. Возведем в квадрат: Ответ: 3.
↑
Задание 6 № 282852
тип B6 В ромбе
ABCD
угол ACD
равен 43°. Найдите угол ABC.
Ответ дайте в градусах.
Решение.
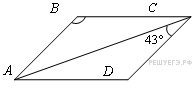 Диагональ
ромба AC
является биссектрисой угла С,
поэтому он равен 86°. Сумма углов B
и C
равна 180°, поэтому искомый угол B
равен 94°.
Диагональ
ромба AC
является биссектрисой угла С,
поэтому он равен 86°. Сумма углов B
и C
равна 180°, поэтому искомый угол B
равен 94°.
Ответ: 94.
↑
Задание 7 № 26764 тип
B7 Найдите
значение выражения
![]() .
Решение.
Выполним
преобразования
.
Решение.
Выполним
преобразования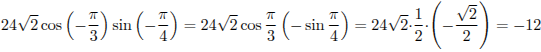 .
.
Ответ: -12.
↑ Задание 8 № 317539 тип B8 На рисунке изображён график функции и восемь точек на оси абсцисс: , , , , . В скольких из этих точек производная функции положительна?

Решение.Положительным
значениям производной соответствует
интервалы, на которых функция
![]() возрастает.
На них лежат точки
возрастает.
На них лежат точки
![]() Таких
точек 5. Ответ:5.
Таких
точек 5. Ответ:5.
↑ Задание 9 № 914 тип B9
 В
правильной четырехугольной пирамиде
точка
—
центр основания,
—
вершина,
В
правильной четырехугольной пирамиде
точка
—
центр основания,
—
вершина,
![]() ,
,
![]() .
Найдите длину отрезка
.
Решение.
В
правильной пирамиде вершина проецируется
в центр основания, следовательно, SO
является высотой пирамиды. Тогда по
теореме Пифагора
.
Найдите длину отрезка
.
Решение.
В
правильной пирамиде вершина проецируется
в центр основания, следовательно, SO
является высотой пирамиды. Тогда по
теореме Пифагора
![]()
Ответ: 16.
Задание 10 № 320172 тип B10
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. Решение. Рассмотрим события
А = кофе закончится в первом автомате, В = кофе закончится во втором автомате.
Тогда
A·B = кофе закончится в обоих автоматах, A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,3; P(A·B) = 0,12. События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52. Ответ: 0,52.
Приведем другое решение. Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятость х = 0,52. Примечание. Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако по условию эта вероятность равна 0,12.
↑ Задание 11 № 25601 тип B11
 Найдите
площадь поверхности многогранника,
изображенного на рисунке (все двугранные
углы прямые).
Решение.
Площадь
поверхности заданного многогранника
равна площади поверхности прямоугольного
параллелепипеда с ребрами 3, 5, 5:
Найдите
площадь поверхности многогранника,
изображенного на рисунке (все двугранные
углы прямые).
Решение.
Площадь
поверхности заданного многогранника
равна площади поверхности прямоугольного
параллелепипеда с ребрами 3, 5, 5:
![]() .
.
Ответ: 110.
↑ Задание 12 № 43145 тип B12
Находящийся
в воде водолазный колокол, содержащий
![]() молей
воздуха при давлении
молей
воздуха при давлении
![]() атмосферы,
медленно опускают на дно водоeма. При
этом происходит изотермическое сжатие
воздуха. Работа, совершаемая водой при
сжатии воздуха, определяется выражением
атмосферы,
медленно опускают на дно водоeма. При
этом происходит изотермическое сжатие
воздуха. Работа, совершаемая водой при
сжатии воздуха, определяется выражением
![]() (Дж),
где
(Дж),
где
![]() —
постоянная,
К —
температура воздуха,
—
постоянная,
К —
температура воздуха,
![]() (атм) —
начальное давление, а
(атм) —
начальное давление, а
![]() (атм) —
конечное давление воздуха в колоколе.
До какого наибольшего давления
можно
сжать воздух в колоколе, если при сжатии
воздуха совершается работа не более
чем 29 100 Дж? Ответ приведите в
атмосферах.
Решение.
Задача
сводится к решению неравенства
(атм) —
конечное давление воздуха в колоколе.
До какого наибольшего давления
можно
сжать воздух в колоколе, если при сжатии
воздуха совершается работа не более
чем 29 100 Дж? Ответ приведите в
атмосферах.
Решение.
Задача
сводится к решению неравенства
![]() при
заданных значениях постоянной
при
заданных значениях постоянной
![]() ,
температуры воздуха
К,
начального давления
атм
и количества воздуха
моль:
,
температуры воздуха
К,
начального давления
атм
и количества воздуха
моль:
![]() атм.
атм.
Значит, наибольшее давление, до которого можно сжать воздух в колоколе, равно 7 атмосферам.
Ответ: 7.
↑ Задание 13 № 111867 тип B13
Грузовик перевозит партию щебня массой 60 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 4 тонны щебня. Определите, сколько тонн щебня было перевезено за пятый день, если вся работа была выполнена за 8 дней. Решение. Пусть в первый день грузовик перевез тонны щебня, во второй — , …, в последний — тонн; всего было перевезено тонн; норма перевозки увеличивалась ежедневно на тонн. Поскольку
.
Имеем
.
Следовательно, за пятый день было перевезено 8 тонн щебня.
Ответ: 8.
↑
Задание 14 № 77490
тип B14
Найдите точку максимума функции
![]() .
Решение.
Заметим,
что
.
Область определения функции — открытый
луч
.
Решение.
Заметим,
что
.
Область определения функции — открытый
луч
![]() .
Найдем производную заданной функции:
.
Найдем производную заданной функции:
![]() Найдем нули
производной:
Найдем нули
производной:

Найденные точки лежит на луче . Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума .
Ответ: 1.
Начало формы
Задание С1 № 500815
а) Решите уравнение
![]() .
б) Найдите все корни этого уравнения,
принадлежащие промежутку
.
б) Найдите все корни этого уравнения,
принадлежащие промежутку
![]() .
.
Решение.
а)
Так как
![]() ,
имеем:
,
имеем:
![]() ,
,
![]() .
Корни уравнения:
.
Корни уравнения:
![]()
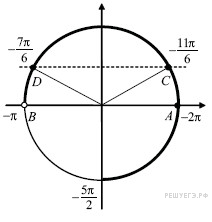 б)
Корни уравнения
изображаются
точками
и
,
а корни уравнения
б)
Корни уравнения
изображаются
точками
и
,
а корни уравнения
![]() —
точками
и
,
промежуток
изображается
жирной дугой (см. рис.). В указанном
промежутке содержатся три корня
уравнения:
—
точками
и
,
промежуток
изображается
жирной дугой (см. рис.). В указанном
промежутке содержатся три корня
уравнения:
![]() и
и
![]() .
.
Ответ:а)
![]() б)
б)
![]()
Задание С2 № 484568
Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка M — середина бокового ребра пирамиды AP.
Решение.
Пусть отрезок PH — высота пирамиды PABCD, отрезок MN — средняя линия треугольника APH (см. рисунок). Поскольку PABCD — правильная пирамида, точка H — центр квадрата ABCD, значит, и , откуда . Но, , следовательно, . Таким образом, прямая BN — проекция прямой BM на плоскость BDP, значит, угол мужду прямой BM и плоскостью BDP равен углу между прямой BM и прямой BN, т. е. острому углу MBN прямоугольного треугольника MBN.
Примем длину ребра данной пирамиды за 1, тогда , , и, следовательно,
, .
Ответ: .
Задание С3 № 500020
Решите
систему неравенств
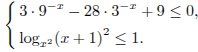
Решение.
1.
Решим первое неравенство системы.
Сделаем замену
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
Тогда
![]() ,
откуда находим решение первого неравенства
системы:
,
откуда находим решение первого неравенства
системы:
![]() .
2. Решим второе неравенство
системы. Рассмотрим два случая.
Первый
случай:
.
2. Решим второе неравенство
системы. Рассмотрим два случая.
Первый
случай:
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Учитывая
условие
,
получаем:
![]() .
Второй случай:
.
Второй случай:![]() .
.
;
![]() ;
;
;
;
![]() .
.
Учитывая
условие
,
получаем
![]() ;
;
![]() .
Решение второго неравенства системы:
;
;
.
3. Решение исходной системы
неравенств:
.
Решение второго неравенства системы:
;
;
.
3. Решение исходной системы
неравенств:
![]() ;
;
.
;
;
.
Ответ:
![]() ;
;
![]() ;
;
![]() .
.
Задание С4 № 484623
На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ABP, проведённую из вершины A, если известно, что сторона квадрата равна 1.
Решение.
Пусть точки Р и А лежат по одну сторону от прямой CD (рис. 1). Треугольник BCP — равнобедренный (BC = CD = CP = 1), поэтому
![]() ,
,
значит,
![]() .
.
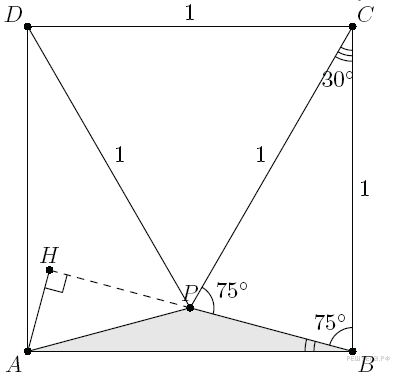
Пусть AH — высота треугольника ABP. Из прямоугольного треугольника ABH находим, что
![]() .
.
Пусть теперь точки P и A лежат по разные стороны от прямой CD (рис.2). Треугольник BCP — равнобедренный (BC = CD = CP = 1), поэтому
![]() ,
значит,
,
значит,
![]()
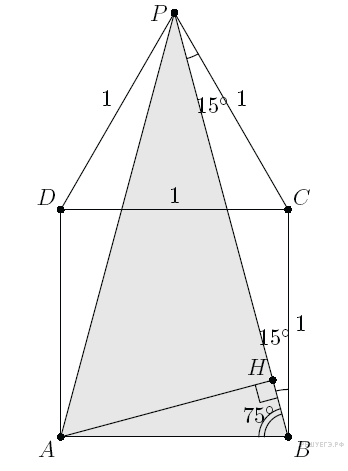
Из прямоугольного треугольника ABH находим, что
![]() .
.
Ответ:
![]() или
или
![]() .
.
Задание С5 № 500390
Найдите
все значения
,
при каждом из которых уравнение
![]() имеет
более двух корней.
имеет
более двух корней.
Решение.
Рассмотрим
функции
![]() и
и
![]() .
Исследуем уравнение
.
На промежутке
.
Исследуем уравнение
.
На промежутке
![]() функция
возрастает.
Функция
убывает
на этом промежутке, поэтому уравнение
имеет
не более одного решения на промежутке
,
причем решение будет существовать тогда
и только тогда, когда,
функция
возрастает.
Функция
убывает
на этом промежутке, поэтому уравнение
имеет
не более одного решения на промежутке
,
причем решение будет существовать тогда
и только тогда, когда,
![]() ,
то есть при
.
При
уравнение
принимает
вид
,
то есть при
.
При
уравнение
принимает
вид
![]() .
При
.
При
![]() левая
часть этого уравнения отрицательна,
следовательно, решений нет. При
левая
часть этого уравнения отрицательна,
следовательно, решений нет. При
![]() это
уравнение сводится к квадратному
уравнению
это
уравнение сводится к квадратному
уравнению
![]() дискриминант
которого
дискриминант
которого
![]() ,
поэтому при
,
поэтому при
![]() это
уравнение не имеет корней; при
это
уравнение не имеет корней; при
![]() уравнение
имеет единственный корень, равный ;
при
уравнение
имеет единственный корень, равный ;
при
![]() уравнение
имеет два корня.
Пусть уравнение
имеет два корня,
уравнение
имеет два корня.
Пусть уравнение
имеет два корня,
![]() и
и
![]() .
.
Тогда
меньший корень
![]() всегда
меньше
всегда
меньше
![]() ,
а больший корень
не
превосходит
,
если
,
а больший корень
не
превосходит
,
если
![]() ,
то есть при
,
то есть при
![]() .
По теореме Виета:
.
По теореме Виета:
![]() ,
,
![]() ,
,
поэтому
знаки корней
и
зависят
от знаков выражений
![]() и
и
![]() .
Значит, при
.
Значит, при
![]() оба
корня отрицательны, при
оба
корня отрицательны, при
![]() один
из корней отрицательный, а другой
неотрицательный, при
один
из корней отрицательный, а другой
неотрицательный, при
![]() оба
корня неотрицательны.
Таким
образом, при
уравнение
не
имеет корней при
и
,
имеет один корень при
оба
корня неотрицательны.
Таким
образом, при
уравнение
не
имеет корней при
и
,
имеет один корень при
![]() и
и
![]() ,
имеет два корня при
.
Таким образом, уравнение
имеет
следующее количество корней:
—
нет корней при
;
— один корень при
и
;
— два корня при
,
имеет два корня при
.
Таким образом, уравнение
имеет
следующее количество корней:
—
нет корней при
;
— один корень при
и
;
— два корня при
![]() и
;
— три корня при
.
Ответ:
.
и
;
— три корня при
.
Ответ:
.
Задание С6 № 500197
Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары групп находят модуль разности найденных сумм и полученные 6 чисел складывают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Каково наименьшее возможное значение полученного результата?
Решение.
Обозначим
суммы чисел в группах
![]() ,
,
![]() ,
,
![]() ,
,
![]() а
указанную в условии сумму модулей их
попарных разностей через
.
Можно считать, что
а
указанную в условии сумму модулей их
попарных разностей через
.
Можно считать, что
![]() .
а) Чтобы число
равнялось
0, необходимо, чтобы каждая из разностей
.
а) Чтобы число
равнялось
0, необходимо, чтобы каждая из разностей
![]() равнялась
0, то есть
равнялась
0, то есть
![]() .
Сумма всех двенадцати чисел
.
Сумма всех двенадцати чисел
![]() .
С другой стороны, она равна
.
С другой стороны, она равна
![]() ,
но 78 не делится на 4. Значит,
,
но 78 не делится на 4. Значит,
![]() .
б) Чтобы число
равнялось
1, необходимо, чтобы все, кроме одной,
разности
равнялись
0. Значит,
.
б) Чтобы число
равнялось
1, необходимо, чтобы все, кроме одной,
разности
равнялись
0. Значит,
![]() ,
но в этом случае каждая из сумм
,
не
равна хотя бы одной из сумм
,
поэтому
хотя бы три разности
не
равны 0 и число
,
но в этом случае каждая из сумм
,
не
равна хотя бы одной из сумм
,
поэтому
хотя бы три разности
не
равны 0 и число
![]() не
меньше 3. Значит,
не
меньше 3. Значит,
![]() .
в) Выразим число
явно
через
,
,
,
:
.
в) Выразим число
явно
через
,
,
,
:
![]()
В
предыдущих пунктах было показано, что
![]() .
Если
.
Если
![]() ,
то
,
то
![]() или
или
![]() .
В этом случае сумма всех двенадцати
чисел равна
.
В этом случае сумма всех двенадцати
чисел равна
![]() или
или
![]() ,
то есть нечётна, что неверно.
Для
следующего разбиения чисел на группы:
,
то есть нечётна, что неверно.
Для
следующего разбиения чисел на группы:
![]() ;
;
![]() ;
;
![]() ;
;
![]() —
число
равно
4.
Ответ: а) нет; б) нет; в) 4.
—
число
равно
4.
Ответ: а) нет; б) нет; в) 4.
Конец формы
