Проверка части с
Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь указанными критериями.
Начало формы
Задание С1 № 484547
Решите уравнение
.
Решение.
Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю и не теряет смысла. Поэтому данное уравнение равносильно системе:
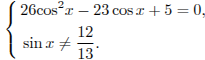
Решив
уравнение системы как квадратное
относительно
,
находим
либо
.
Если
,
то
и
условие
выполняется.
Следовательно,
.
Если
,
то
.
В этом случае с учетом неравенства
системы
получаем, что из двух точек единичной
окружности, соответствующих решениям
уравнения
,
нужно оставить только ту, для которой
.
Это точка четвертой четверти, и решение
уравнении имеет вид
.
Ответ: ; .
Задание С2 № 484567
В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
Решение.
Вместо
прямой CD
рассмотрим параллельную ей прямую BE.
Искомый угол равен углу SBE.
Треугольник SBE
равносторонний, поскольку большая
диагональ правильного шестиугольника
вдвое больше его стороны:
.
Следовательно,
.
Ответ:
.
Задание С3 № 485950
Решите систему неравенств:
Решение.
Рассмотрим
второе неравенство. Оно имеет смысл при
т.
е. при
Пусть
Тогда
неравенство принимает вид
откуда
.
Имеем:
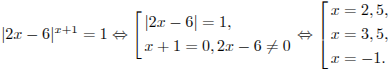
Подставим
в первое неравенство найденные значения
:
1. При
:
2.
При
:
3.
При
:
Неравенству
удовлетворяют значения
и
Ответ:
;
Задание С4 № 484612
В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону BC точками M и N так, что . Найдите BC если .
Решение. Пусть E — точка пересечения биссектрис, BM=x, MN=y NC=z. Так как , то точка M лежит между точками B и N возможны 2 случая. 1. Точка E — внутри параллелограмма. Треугольники ABN и DMC равнобедренные, следовательно, , откуда, .
2. Точка E — вне параллелограмма. Тогда , откуда .
Ответ: 16 или 48.
Задание С5 № 484628 Найдите все значения a при каждом из которых система не имеет решений.
Решение.
Рассмотрим второе неравенство системы .
Если , то неравенство, а значит, и система не имеет решений. Если , то решение неравенства — луч .
Если , то решение неравенства — луч .
При первое неравенство системы принимает вид
Если , то решение этой системы — два луча с концами в точках .
Если , то решение этой системы — полуинтервал с концами в точках .
Отметим, что точки нет в множестве решений второго неравенства. Для того, чтобы система не имела решений, при необходимо и достаточно:
.
Ответ: .
Задание С6 № 484664
Найдите
все простые числа p,
для каждого из которых существует такое
целое число k,
что число p
является общим делителем чисел
и
.
Решение.
Если
число p
является делителем числа
,
то оно является также и делителем числа
.
Но если число p
является общим делителем чисел
и
,
то оно является также и делителем
разности этих чисел, то есть числа
.
Аналогично
получаем:
1) число p
является общим делителем чисел
и
,
значит, p
является делителем числа
;
2)
число p
является общим делителем чисел
и
,
значит, p
является делителем числа
;
Число
105 имеет ровно три различных простых
делителя — 3, 5 и 7. Остается проверить
найдутся ли такие целые числа k
для каждого из которых одно из чисел 3,
5 и 7 является общим делителем чисел
и
.
Если
,
то число 3 является общим делителем
данных чисел. Если число k
кратно 5, то число 5 является общим
делителем данных чисел. Если число k
кратно 7, то число 7 является общим
делителем данных чисел.
Замечание.
Последние два условия могут быть
объединены в одно: если число k
кратно 35, то числа 5 и 7 являются общими
делителями данных чисел.
Ответ:
3, 5, 7.