Результаты Вариант № 275
№ п/п |
Номер |
Тип |
Правильный ответ |
1 |
24805 |
B1 |
6 |
2 |
27528 |
B2 |
3 |
3 |
27609 |
B3 |
2 |
4 |
26673 |
B4 |
700 |
5 |
106891 |
B5 |
-1,25 |
6 |
27261 |
B6 |
3,75 |
7 |
26735 |
B7 |
33 |
8 |
317543 |
B8 |
-2 |
9 |
923 |
B9 |
45 |
10 |
320173 |
B10 |
0,02 |
11 |
27080 |
B11 |
6 |
12 |
27998 |
B12 |
30 |
13 |
26596 |
B13 |
20 |
14 |
286603 |
B14 |
6 |
↑Задание 1 № 24805 тип B1 Сырок стоит 8 рублей 20 копеек. Какое наибольшее число сырков можно купить на 50 рублей?
Решение.
Разделим
50 на 8,2:
Значит, на 50 рублей можно
купить 6 сырков.
Ответ: 6.
↑Задание 2 № 27528 тип B2
Н
а
рисунке жирными точками показано
суточное количество осадков, выпадавших
в Томске с 8 по 24 января 2005 года. По
горизонтали указываются числа месяца,
по вертикали — количество осадков,
выпавших в соответствующий день, в
миллиметрах. Для наглядности жирные
точки на рисунке соединены линией.
Определите по рисунку, сколько дней
выпадало более 2 миллиметров осадков.
Решение.
Видно,
что более 2 миллиметров осадков выпадало
три дня: 8, 12 и 14 января (см. рис.).
О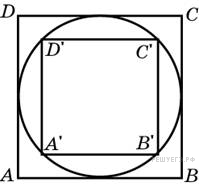
твет:
3.
↑Задание 3 № 27609 тип B3
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность? Решение. Пусть радиус окружности равен R. Тогда сторона описанного вокруг нее квадрата равна 2R, а его площадь, равная квадрату стороны, равна 4R2. Диагональ вписанного квадрата также равна 2R, поэтому его площадь, равная половине произведения диагоналей, равна 2R2. Следовательно, отношение площади описанного квадрата к площади вписанного равно 2.
Ответ: 2.
↑Задание 4 № 26673 тип B4
Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
Тарифный план |
Абонентская плата |
Плата за трафик |
План «0» |
Нет |
2,5 руб. за 1 Мб |
План «500» |
550 руб. за 500 Мб трафика в месяц |
2 руб. за 1 Мб сверх 500 Мб |
План «800» |
700 руб. за 800 Мб трафика в месяц |
1,5 руб. за 1 Мб сверх 800 Мб |
Пользователь
предполагает, что его трафик составит
600 Мб в месяц и, исходя из этого,
выбирает наиболее дешевый тарифный
план. Сколько рублей заплатит пользователь
за месяц, если его трафик действительно
будет равен 600 Мб?
Решение.
Рассмотрим
все варианты.
По Плану «0» пользователь
потратит 2,5 
600 = 1500 руб.
в месяц за 600 Мб трафика.
По плану
«500» он потратит 550 руб. абонентской
платы за 500 Мб и 2
100 = 200 руб.
сверх того. Поэтому полная плата в месяц
составит 550 + 200 = 750 руб.
По
плану «800» пользователь потратит в месяц
за 600 Мб трафика 700 руб.
Наиболее
выгодный вариант составляет 700 руб.
Ответ: 700.
↑Задание
5 № 106891 тип B5
Найдите корень уравнения:
.
Решение.
Последовательно
получаем:
.
Ответ: −1,25.
↑Задание
6 № 27261 тип B6
В треугольнике
угол
равен
90°,
,
.
Найдите высоту
.
Решение.
Углы
и
равны
как углы со взаимно перпендикулярными
сторонами. Тогда
.
Ответ: 3,75.
↑Задание
7 № 26735 тип B7Найдите
значение выражения
.
Решение.
Выполним
преобразования:
Ответ:
33.
↑Задание
8 № 317543 На
рисунке изображен график функции
и
отмечены точки −2, −1, 1, 2. В какой из этих
точек значение производной наибольшее?
В ответе укажите эту точку.
Решение. Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная положительна в точках −2 и 2. Угол наклона (и его тангенс) явно больше в точке −2.
Ответ:−2.
↑
Задание
9 № 923 В
правильной треугольной пирамиде
–
середина ребра
,
–
вершина. Известно, что
=5,
а
=6.
Найдите площадь боковой поверхности
пирамиды.
Решение.
отрезок
является
медианой правильного треугольника
,
а значит, и его высотой. Тогда
Ответ:
45.
↑Задание 10 № 320173 тип B10 (решено неверно или не решено)
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых. Решение. Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна
Ответ:
0,02.
↑Задание 11 № 27080
Три
ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 4, 6,
9. Найдите ребро равновеликого ему куба.
Решение.
Объем
куба
равен
объему параллелепипеда
Значит, ребро
куба
Ответ:
6.
↑Задание 12 № 27998
Мяч
бросили под углом
к
плоской горизонтальной поверхности
земли. Время полeта мяча (в секундах)
определяется по формуле
.
При каком наименьшем значении угла
(в
градусах) время полeта будет не меньше
3 секунд, если мяч бросают с начальной
скоростью
м/с?
Считайте, что ускорение свободного
падения
м/с
.
Решение.
Задача
сводится к решению неравенства
на
интервале
при
заданных значениях начальной скорости
и ускорения свободного падения:
.
Ответ:
30.
↑Задание 13 № 26596
Двое
рабочих, работая вместе, могут выполнить
работу за 12 дней. За сколько дней, работая
отдельно, выполнит эту работу первый
рабочий, если он за два дня выполняет
такую же часть работы, какую второй –
за три дня?
Решение.
Обозначим
и
–
объёмы работ, которые выполняют за день
первый и второй рабочий, соответственно,
полный объём работ примем за 1. Тогда по
условию задачи
и
.
Решим полученную систему:
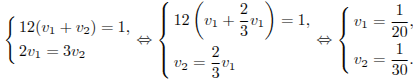
Тем самым, первый рабочий за день выполняет одну двадцатую всей работы, значит, работая отдельно, он справится с ней за 20 дней.
Ответ: 20.
Задание
14 № 286603
Найдите точку максимума функции
.
Решение.
Квадратный
трехчлен
с
отрицательным старшим коэффициентом
достигает максимума в точке
,
в нашем случае — в точке 6.
Поскольку функция
возрастающая,
а заданная функция определена при
найденном значении переменной, она
достигает максимума в той же точке, в
которой достигает максимума подкоренное
выражение.
Ответ: 6.
Задание С1 № 500192
Критерии оценивания выполнения задания |
Баллы |
Обоснованно получены верные ответы в обоих пунктах |
2 |
Обоснованно получен верный ответ в пункте а или в пункте б |
1 |
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
Максимальный балл |
2 |
а)
Решите уравнение
б)
Найдите все корни этого уравнения,
принадлежащие отрезку
.
Решение.
а) Запишем уравнение в виде
Значит,
или
,
откуда
,
,
или
,
откуда
или
,
.
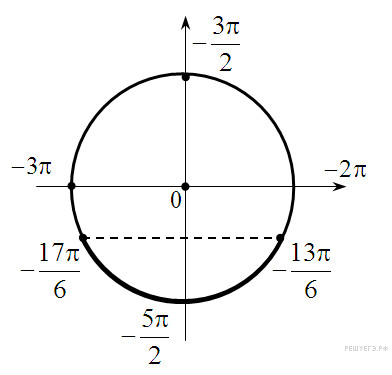
б) С помощью числовой окружности
отберем корни уравнения, принадлежащие
отрезку
.
Получим числа:
,
и
.
Ответ: а)
,
;
,
,
;
б)
,
и
Задание С2 № 500898
Критерии оценивания выполнения задания |
Баллы |
Обоснованно получен верный ответ |
2 |
Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено |
1 |
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
Максимальный балл |
2 |
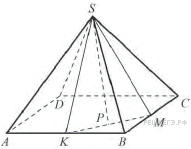
В
правильной четырехугольной пирамиде
с
основанием
проведено
сечение через середины ребер
и
и
вершину
найдите
площадь этого сечения, если все ребра
пирамиды равны 8.
Решение.
Изобразим
указанное в условии сечение — треугольник
Проведем
в треугольнике
высоту
Точка
—
.
Значит,
Из
треугольника
находим
Из
треугольника
находим
Тогда
Ответ:
Задание С3 № 484580
Критерии оценивания выполнения задания |
Баллы |
Обоснованно получен верный ответ |
3 |
Обоснованно получен ответ, отличающийся от верного только конченым числом точек |
2 |
Полученный ответ неверен, но решение содержит переход от исходного неравенства к верным рациональным неравенствам |
1 |
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
Максимальный балл |
3 |
Решите
неравенство
.
Решение.
Пусть
,
тогда неравенство прини-мает вид:
.
Очевидно
поэтому
т.
е.
.
Получаем:
.
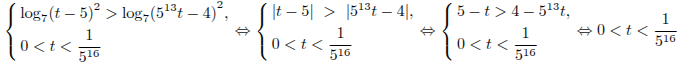Тогда
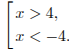
Ответ:
,
.
Задание С4 № 484612
Критерии оценивания выполнения задания |
Баллы |
Рассмотрены все возможные геометрические конфигурации, и получен правильный ответ |
3 |
Рассмотрена хотя бы одна возможная конфигурация, в которой получено правильное значение искомой величины |
2 |
Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за геометрической ошибки |
1 |
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
Максимальный балл |
3 |
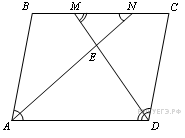
В
параллелограмме ABCD
биссектрисы углов при стороне AD
делят сторону BC
точками M
и N
так, что
.
Найдите BC
если
.
Решение.Пусть
E —
точка пересечения биссектрис, BM=x,
MN=yNC=z.
Так как
,
то точка M
лежит между точками B
и Nвозможны
2 случая.
1. Точка E —
внутри параллелограмма. Треугольники
ABN
и DMC
равнобедренные,
следовательно,
,
откуда,
.
2.
Точка E —
вне параллелограмма. Тогда
,
откуда
.
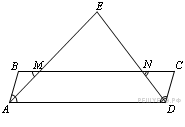
Ответ: 16 или 48.
Вопрос НЕ сказано как располагаются точки M и N => можно поменять местами и решить ещё два случая
Ответ Если поменять местами точки M и N, то станет невозможным выполнение условия BM:MN = 1:2.
Задание С5 № 484644
Критерии оценивания ответа на задание С5 |
Баллы |
Обоснованно получен верный ответ. |
4 |
Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку. |
3 |
Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки. |
2 |
Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок. |
1 |
Все прочие случаи. |
0 |
Максимальное количество баллов |
4 |
Найти
все значения а,
при каждом из которых функция
имеет
более двух точек экстремума.
Решение.
1.
Функция f
имеет вид
а) при
:
,
поэтому ее график есть часть параболы
с ветвями, направленными вверх, и осью
симметрии
;
б) при
:
,
поэтому ее график есть часть параболы
с ветвями, направленными вверх, и осью
симметрии
.
Все возможные виды графиков
функции показаны на рисунках:
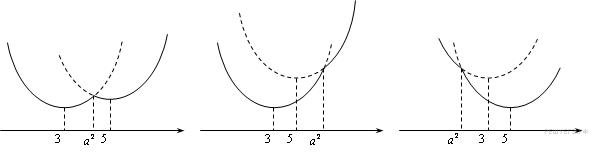
Графики
обеих квадратичных функции проходят
через точку
.
3. Функция
имеет
более двух точек экстремума, а именно
три, в единственном случае (рис. 1):
.
Ответ:
;
.
Задание С6 № 484653
Критерии оценивания ответа на задание С6 |
Баллы |
Обоснованно получен верный ответ. |
4 |
Решение не содержит логических пробелов, получен ответ, неверный только из-за вычислительной ошибки или описки. |
3 |
Решение доведено до ответа, но содержит логические пробелы, вычислительные ошибки или описки. 2 |
2 |
Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок. |
1 |
Все прочие случаи. |
0 |
Максимальное количество баллов |
4 |
Среди
обыкновенных дробей с положительными
знаменателями, расположенных между
числами
и
,
найдите такую, знаменатель которой
минимален.
Решение.Так
как
и
,
то достаточно найти правильную дробь с наименьшим знаменателем, лежащую между числами
и
,
а затем прибавить к ней число 2.
Среди
дробей со знаменателями 2, 3, 4, 5 и 6 нужных
дробей нет, так как
,
,
,
,
,
,
,
.Для
знаменателя 7 получаем
,
т. е.
.
Ответ:
.
Конец формы