§ 15.7. Переходные процессы дискретных систем

Показатели качества дискретных (естественно, устойчивых) систем и методы их исследования практически полностью аналогичны случаю непрерывных систем. Это касается управляемости, наблюдаемости, астатизма, показателей качества в переходном и установившемся режимах. Поэтому на методах исследования управляемости, наблюдаемости и определения показателей качества дискретных систем здесь останавливаться не будем. Рассмотрим лишь отличительные особенности и порядок построения переходных процессов дискретных систем.

Условия конечной длительности. Одной из важных особенностей дискретных систем является возможность обеспечения переходных процессов конечной длительности. Такой переходной процесс длится ровно n периодов квантования, где n – порядок системы. Условия существования переходного процесса конечной длительности определяются следующей теоремой.

Теорема. Если знаменатель передаточной функции дискретной системы по некоторому воздействию равен , т.е.

. (15.54)

то переходный процесс данной системы по этому воздействию длится ровно n периодов T квантования по времени. ■

Пример 15.13. Найти длительность переходного процесса дискретной системы с передаточной функцией при и нулевых начальных условиях, если с.

Решение. Воспользуемся рекуррентным методом решения разностных уравнений. В данном случае это уравнение имеет вид . Разделим обе его части на и перейдём к оригиналам. В результате получим .

Полагая последовательно в этом выражении , будем иметь Как видно, в полном соответствии с условием (15.54), через три такта выходная переменная принимает установившееся значение 0,9; т.е. переходный процесс длится ровно три периода квантования по времени, и его длительность с. При этом предыдущие значения выходной переменной не влияют на её последующие значения ни при каком k. ■

Условие (15.54) приведенной теоремы, при котором обеспечивается конечная длительность переходных процессов дискретных систем, часто применяется при создании систем управления с заданной длительностью переходных процессов. Иногда такие дискретные системы называются оптимальными по быстродействию.

Для построения переходных процессов дискретных систем, как и непрерывных, целесообразно использовать ЭВМ. Приведём некоторые примеры.

Пример 15.14. Найти аналитические выражения для переходной h_k и импульсной переходной (весовой) w_k функции дискретной системы, которая описывается уравнениями

, .

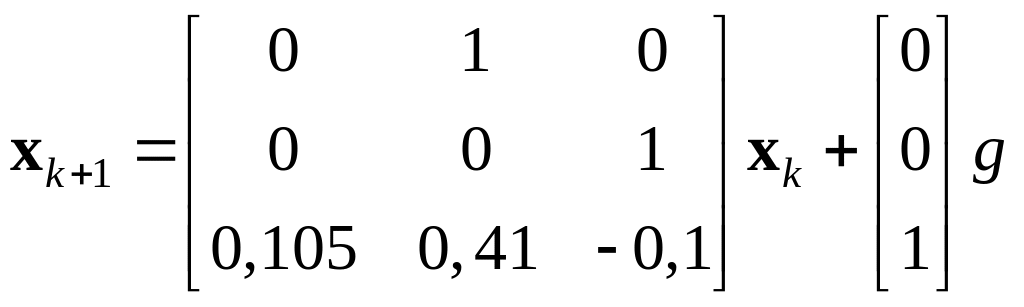Решение в MATLAB:

% команды:

sys = ss([0 1 0;0 0 1;0.105 0.41 -0.1],[0 0 1]',[0.245 0.34 0],0);

sys1 = tf(sys); set(sys1,'Variable','z')

sys1

Transfer function:

0.34 z + 0.245

------------------------------

z^3 + 0.1 z^2 - 0.41 z - 0.105

% затем вводим следующие команды:

syms z k

hk=iztrans((.34*z+.245)*z/((z^2+.8*z+.15)*(z-.7)*(z-1)),k)

wk=iztrans((.34*z+.245)/((z^2+.8*z+.15)*(z-.7)),k)

% результаты:

hk =

11/20*(-3/10)^k-5/24*(-1/2)^k-161/120*(7/10)^k+1

wk = -7/3*charfcn[0](k)+143/60*(-3/10)^k-5/8*(- -1/2)^k+23/40*(7/10)^k

Следовательно

.

Выражение для w_k выдаваемое MATLAB имеет ряд особенностей. В частности, charfcn[0](k) – это обозначение в системе MATLAB дискретной δ-функции δ(k). Поэтому выражение для w_k формально имеет вид

.

Однако такое выражение не может соответствовать весовой функции рассматриваемой системы с физической точки зрения. Это связано с тем, что в реакции системы, числитель передаточной функции которой меньше степени знаменателя, не может содержаться составляющая, пропорциональная δ-функции. К этому же выводу можно прийти, если w_k найти как разность h_k – h_{k – 1}. Поэтому для получения выражения, которое корректно описывает весовую функцию, необходимо преобразовать выданное MATLAB выражение (к переменной k – 1) следующим образом:

, .

При этом оба приведённых выражения дают, естественно, одни и те же значения w_k при всех k = 0, 1, 2, … . ■

В ряде случаев необходимо получить только графики переходной h_k и импульсной переходной (весовой) w_k функций дискретных систем. Для этой цели MATLAB используется следующим образом.

Пример 15.15. Построить графики переходной h_k и импульсной переходной (весовой) w_k функций дискретной системы, передаточная функция которой имеет вид

,

а период квантования Т = 1,2.

Решение в MATLAB:

% команды:

sys=tf ([0.34 0.245],[1 0.1 0.695 -0.105], 1.2);

step(sys)

impulse(sys)

Графики, выданные MATLAB, приведены на рис. 15.15. ■

Пример 15.16. Построить графики переходной h_k и импульсной переходной (весовой) w_k функций дискретной системы, заданной уравнениями в переменных состояния

, , где

, , , ,

а период квантования Т = 0,3.

Решение в MATLAB:

% команды:

sys=ss([-3 2;1 -2],[0;1],[2 0], 0, 0.3);

step(sys)

impulse(sys)

Графики функций h_k и w_k и в этом случае имеют вид, аналогичный приведённым на рис. 15.15. ■

Замечание. На графиках рис. 15.15, выданных MATLAB, значениям функций h_k и w_k соответствуют лишь отрезки вертикальных линий при . Остальные линии являются ничем не обоснованной экстраполяцией этих значений.