одним выходом:

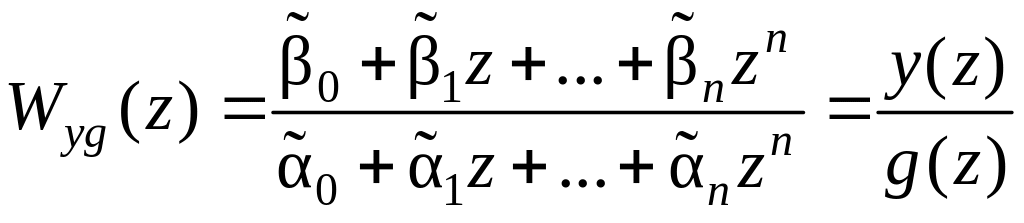. (15.26)

Алгоритм перехода к соответствующим уравнениям в переменных состояния включает следующие шаги:

1. Числитель и знаменатель в (15.26) делится на коэффициент 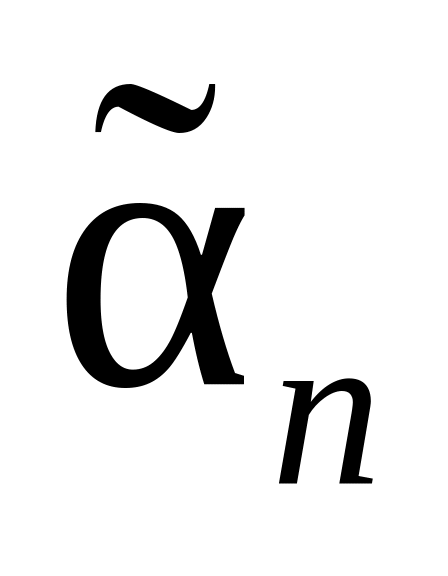. Это даёт

.

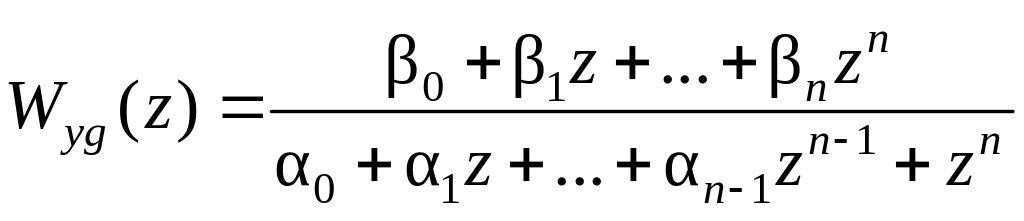2. Если степень числителя в (15.26) меньше степени знаменателя, т.е. , то переход к п. 3 алгоритма. В противном случае (если 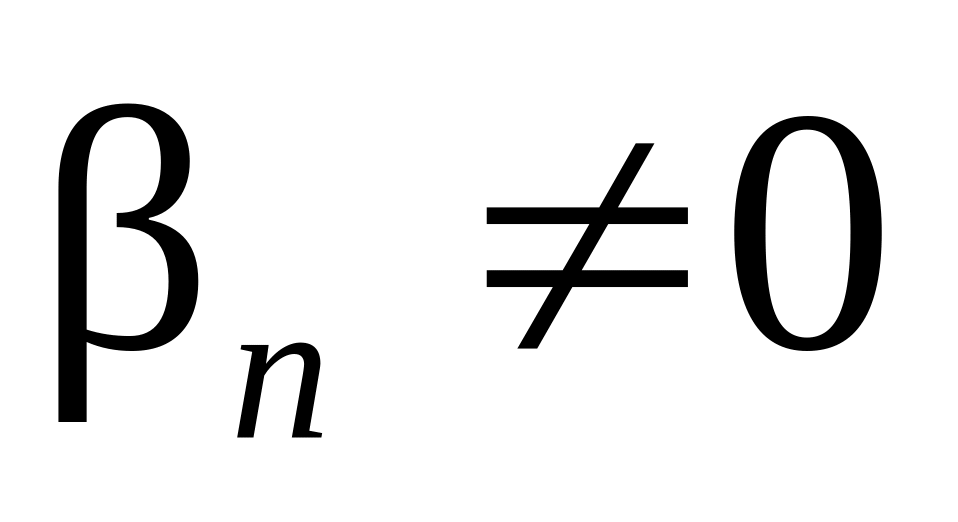) выделяется целая часть (например, делением «в столбик» числителя на знаменатель). Результирующая функция имеет вид

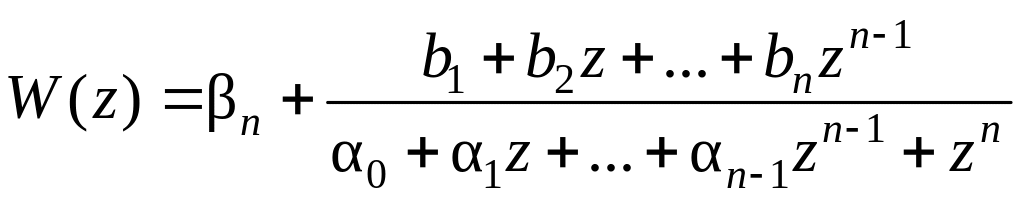, (15.27)

где , .

3. Записывается уравнения дискретной системы в переменных состояния либо в канонической управляемой форме (КУФ):

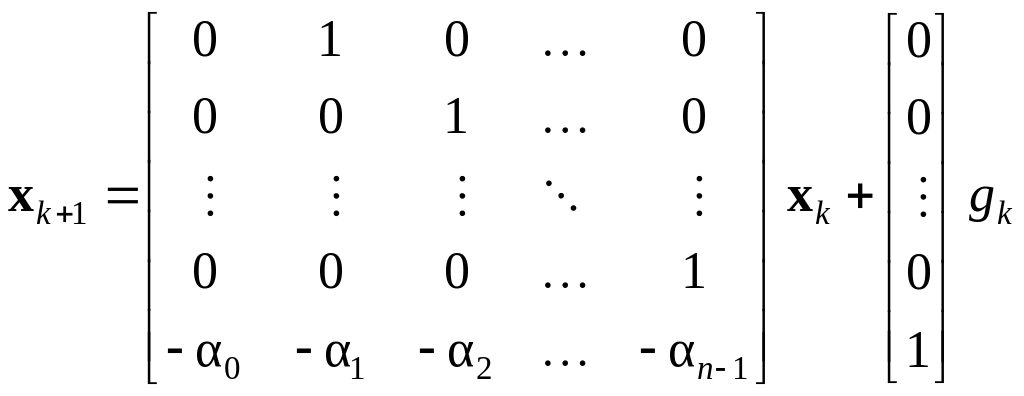, (15.28)

(15.29)

либо в канонической наблюдаемой форме (КНФ)

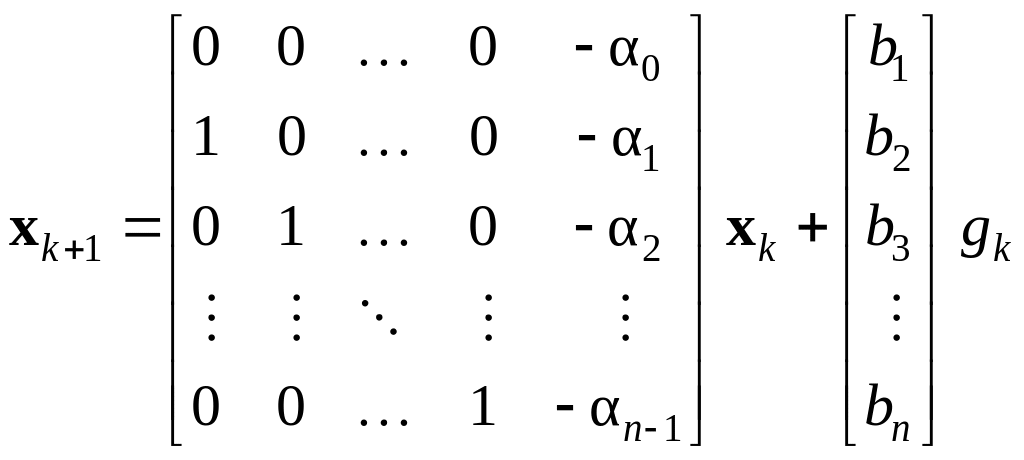, (15.30)

. (15.31)

Подчеркнем, что с точки зрения полноты описания дискретной системы, которая задана лишь своей передаточной функцией (15.26), обе формы уравнений (15.28), ­(15.29) и (15.30), (15.31) – равноценны. При этом к уравнениям в канонической управляемой форме (КУФ) можно добавить любое число уравнений выхода, а к уравнениям в канонической наблюдаемой форме (КНФ) – любое число входов, без изменения коэффициентов предыдущих уравнений.

Пример 15.5. Найти уравнения в переменных состояния импульсной системы, передаточные функции которой имеют вид

, .

Решение. Заданные передаточные функции имеют вид (15.25), одинаковые знаменатели и . Поэтому, прежде всего, в соответствии с алгоритмом перехода, разделим числители и знаменатели , а затем во второй передаточной функции выделим целую часть:

, , .

Далее переходим к шагу 3 алгоритма. В данном случае система имеет два входа , и один выход , поэтому, применяя выражения (15.30), (15.31), соответствующие КНФ, найдём

, . (15.32)

Это и есть уравнения в переменных состояния заданной импульсной системы. ■

Отметим в заключение этого раздела, что квантование по времени в импульсных системах не всегда необходимо учитывать. Оказывается, если частота квантования по времени достаточно высока, то квантованием по времени можно пренебречь. Здесь T – период следования импульсов. Пусть – это граничная частота ПНЧ, т.е. такая частота, что при всех АЧХ ПНЧ практически равна нулю, т.е. при . Тогда, заменяя на , можно установить, что на интервале частот от до выполняется приближенное равенство

, (15.33)

если

. (15.34)

На рис. 15.12 показан процесс образования из АЧХ приведенной непрерывной части. Здесь на интервале частот от до кривая 1 – это АЧХ приведенной непрерывной части. Кривая 2 – это амплитудно-частотная характеристика импульсной системы при , а кривая 3 – это та же характеристика, но при (при условии, что ). Как видно, является периодической по частоте функцией. При этом, если условие (15.34) выполняется и T = 1, то амплитудно-частотная характеристика импульсной системы представляет собой повторяющуюся с периодом АЧХ приведённой непрерывной части. Причем на интервале частот от до эта характеристика совпадает с частотной характеристикой приведенной непрерывной части.

Другими словами, если условие (15.34) выполняется, то квантование сигнала сказывается (при ) лишь на амплитуде выходного сигнала системы в разомкнутом состоянии, т.е. условие (15.34) можно рассматривать как условие непрерывности импульсных систем.

Неравенство (15.34) является основным условием известной теоремы Котельникова.

Поэтому часто говорят, что если период квантования импульсной системы удовлетворяет условиям теоремы Котельникова, то такую импульсную систему можно рассматривать как непрерывную с передаточной функцией . Если же условие (15.34) не выполняется, то АЧХ дискретной системы (кривая 3 на рис. 15.14) на интервале частот от до существенно отличается от АЧХ приведённой непрерывной части (кривая 1(2)). Следовательно, в этом случае квантование по времени существенно сказывается на характере процессов системы и её необходимо анализировать как дискретную систему.

В дальнейшем будем предполагать, что условие (15.34) не выполняется, т.е. рассматриваемые системы должны исследоваться как дискретные.

Итак, математическая модель дискретной системы, как и непрерывной, может быть представлена либо в виде уравнений в переменных состояния (15.14), (15.28), (15.29), (15.30), (15.31), либо в виде уравнений вход-выход (15.15), либо в виде передаточных функций в разомкнутом или в замкнутом состоянии (15.18), (15.23), (15.25). При этом если дискретная система полная, в том же смысле, что и непрерывная, то все эти модели эквивалентны друг другу.

§ 15.5. Решение уравнений дискретных систем

Решения уравнений дискретных систем необходимы для исследования реакций этих систем на различные внешние воздействия при определённых начальных условиях.

Уравнения (15.14) или (15.28), (15.29), по сути дела, являются рекуррентными соотношениями, которые позволяют вычислить последовательно (рекуррентно) значения как переменных состояния, так и выходной величины, соответствующие моментам времени kT. Рассмотрим эту возможность на численном примере.

Пример 15.6. Найти значения при дискретной системы, уравнения которой имеют вид

, . (15.35)

Вектор начальных условий , а входное воздействие является единичной ступенчатой функцией, т.е. .

Решение. Полагая в (15.35) k = 0, получим

, ,

так как . Аналогично при , поэтому

, .

Далее при , по-прежнему, а

, .

Наконец, y₃ = 0,46. Этот процесс можно продолжать сколь угодно долго, что позволяет найти значения x_k и y_k при любых целых k. ■

Если описанный в примере 15.6 процесс осуществить в символьной форме, то из (15.14) получим следующую последовательность:

, , ,

или

,

Обобщая эти выражения, получим следующие соотношения:

, (15.36)

(15.37)

Формулы (15.36) и (15.37) определяют значения выходного сигнала импульсной системы в дискретные моменты времени. Ординаты , естественно, не дают значений внутри периода квантования. Поэтому, если необходимо определить значения системы, приведенной на рис. 15.10, внутри периодов при можно использовать выражение

(15.38)

Здесь – матрица и векторы из уравнений (15.4), (15.5); .

Описанный рекуррентный метод может использоваться и для решения уравнений «вход-выход» дискретных систем.

Большим неудобством рассмотренного рекуррентного метода решения уравнений дискретных систем является то, что для получения любого, скажем, 10-го значения переменной y_k необходимо вычислить все девять предыдущих значений y₁ y₉ . Поэтому для определения реакций дискретных систем при больших значениях k целесообразнее использовать метод z-преобразования. При этом может использоваться любая из приведённых выше моделей дискретных систем. Наиболее удобным является уравнение «вход-выход», записанное с помощью передаточной функции

. (15.39)

Подставляя в это выражение z-изображение g(z) воздействия g_k и передаточную функцию W_yg(z), получим z-изображение дискретной функции y_k . Далее, как отмечалось выше, необходимо вынести z из числителя правой части (15.39), а оставшуюся дробь разложить на сумму простейших дробей. Затем с помощью таблиц z-изображений (см. приложение П.1) найти оригинал – y_k, значения которого равны значениям выходной переменной системы в моменты времени .

Пример 15.7. Найти реакцию системы (15.35) на линейное воздействие при

нулевых начальных условиях и T = 1.

Решение. Так как уравнения (15.35) записаны в канонической управляемой форме

(15.28), (15.29) при , то в соответствии с выражением (15.26) её уравнение «вход-выход» имеет вид

.

По таблице из приложения П.1 находим, что z-изображение заданного входного воздействия при T = 1 определяется равенством

.

Следовательно, в рассматриваемом случае

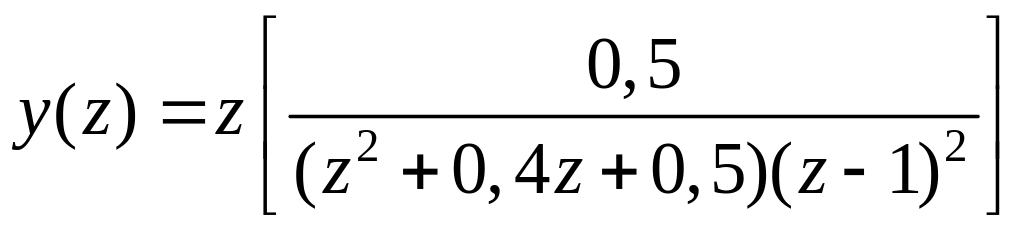. (15.40)

Так как корни полинома – комплексные, то дробь в квадратных скобках представим сначала в виде суммы:

. (15.41)

Для определения коэффициентов запишем систему

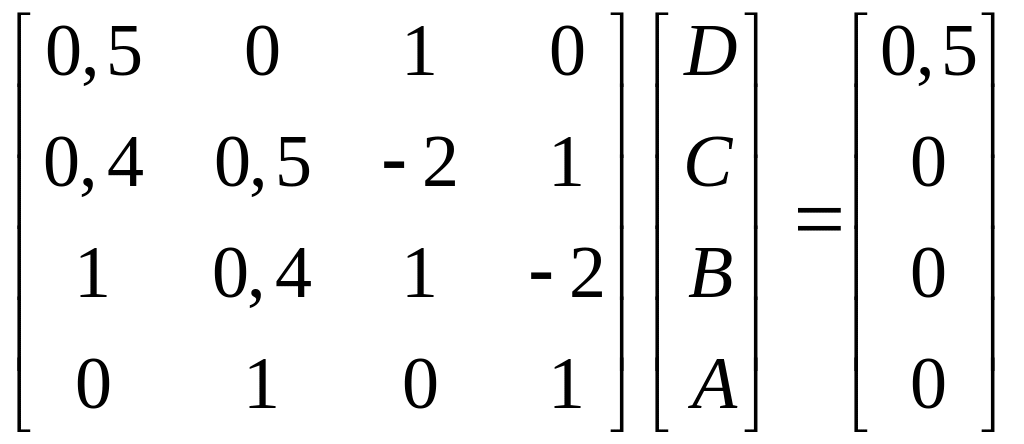. (15.42)

Решение системы (15.42) позволяет с учетом (15.41) представить равенство (15.40) следующим образом:

. (15.43)

Имея в виду 3, 4, 8 и 9-ю строки таблицы из приложения П.1 при ; , , , приведём равенство (15.43) к виду

. (15.44)

Z-изображению (15.44), в соответствии с указанной выше таблицей, соответствует решётчатая функция

. (15.45)

Это равенство, очевидно, позволяет сразу найти реакцию системы (15.35) на воздействие g_k = 0,5k в любой момент времени t_k = kТ, кратный периоду квантования Т. ■

Отметим, что Z-преобразование может применяться и для решения уравнений дискретных систем в переменных состояния типа (15.14). В этом случае получаются аналитические выражения типа (15.45) как для переменных состояния, так и для выходных величин системы. Несомненно, в этом случае объём получаемой информации об исследуемой системе значительно выше, чем при решении уравнений «вход-выход».