§2.6. Формулировка II-го закона термодинамики для изолированных и замкнутых систем

II-й закон термодинамики для изолированных систем:

В изолированных системах общее изменение энтропии всегда неотрицательно (оно переходит в наиболее вероятное состояние):

ΔS≥0 (знак «>» относится к необратимым процессам, а «=» – к обратимым)

изолированная

система

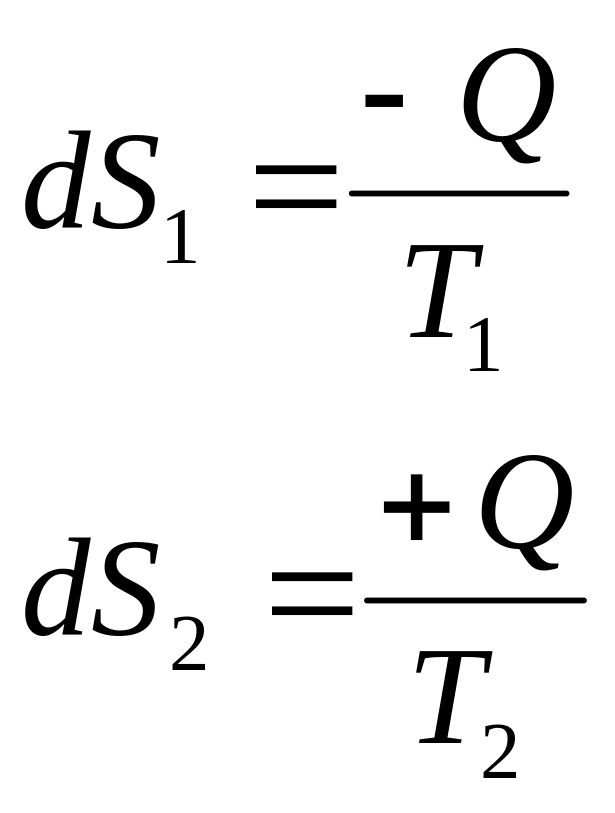
Для замкнутой системы, которая может переходить из состояния 1 в состояние 2, II-й закон термодинамики:

, здесь dQ – подводимое из вне тепло.

Следствие из II-го закона термодинамики:

§2.7. II закон термодинамики и живой организм (для открытой системы)

Согласно Пригожину, полное изменение энтропии открытой системы можно представить в виде двух частей:

ΔS=ΔS_i+ΔS_e

Причина 1-й части (ΔS_i) – внутренние процессы; а ΔS_e – обмен веществом и энергией с окружающей средой (внешние процессы).

ΔG=ΔG_i+ΔG_e ΔG - изменение свободной энергии по Гиббсу

Всегда в реальных системах: ΔS_i>0, ΔG_i<0;

ΔS_e и ΔG_e могут быть и «+» и «–».

Если организм отдает тепло в окружающую среду:

(ΔQ<0, то есть отводится)

В термодинамике вводят при непрерывном изменении энтропии во времени скорость изменения энтропии:

- продукция энтропии,

- поток энтропии.

⇒ II-й закон термодинамики в открытых системах:

В открытых системах продукция энтропии всегда положительна, а внутреннее изменение свободной энергии всегда отрицательно, то есть , .

В изолированной системе: ⇒

§2.8. Стационарное состояние. Теорема Пригожина

Особую роль стационарное состояние.

Стационарное состояние является более выгодным.

Термодинамическое условие стационарного состояния: или (изменение продукции энтропии компенсируется отводом в окружающую среду).

Теорема Пригожина:

В стационарном состоянии продукция энтропии имеет постоянное и минимальное значение, то есть:

КПД системы в стационарном состоянии является максимальным.

Теорема Пригожина справедлива для линейных систем, для систем которые близки к стационарному состоянию.

Глава 3. Кинетика биохимических процессов

Кинетика биохимических процессов с позиции физической химии изучает механизмы физических превращений в зависимости от различных факторов (температура, давление, ph, катализаторы).

§3.1. Основные определения и законы кинетики химических реакций

Пусть в замкнутых системах протекает химическая реакция:

ν₁A₁+ ν₂A₂+… +ν_mA_m ⇄ ν'₁B₁+ ν'₂B₂+…+ ν'_eB_e, (1)

где ν_i – стехиометрические коэффициенты,

A_i – исходные вещества,

B_i – продукты.

Скорость образования или расходования компонента:

, (2)

, (3)

Скорость химической реакции – это величина

(4)

i - любой компонент реакции.

Скорость химической реакции зависит от:

• концентрации реагирующих веществ,

• температуры,

• катализаторов.

Согласно каталитической, скорость химической реакции определяется числом столкновений молекул друг с другом в единицу времени.

В соответствии с теоремой о произведении вероятностей (вероятность любого события, состоящего из нескольких событий, равно произведению вероятностей этих событий), ⇒ скорость химической реакции прямо пропорциональна произведению концентраций в степени их стехиометрических коэффициентов:

– закон действующих масс (5)

k – константа скорости.

Чтобы преодолеть барьер при отталкивании, молекулы должны обладать определенным потенциалом:

E_A – энергия активации.

Доля молекул, обладающих энергией, большей, чем E_A, определяется уравнением Больцмана:

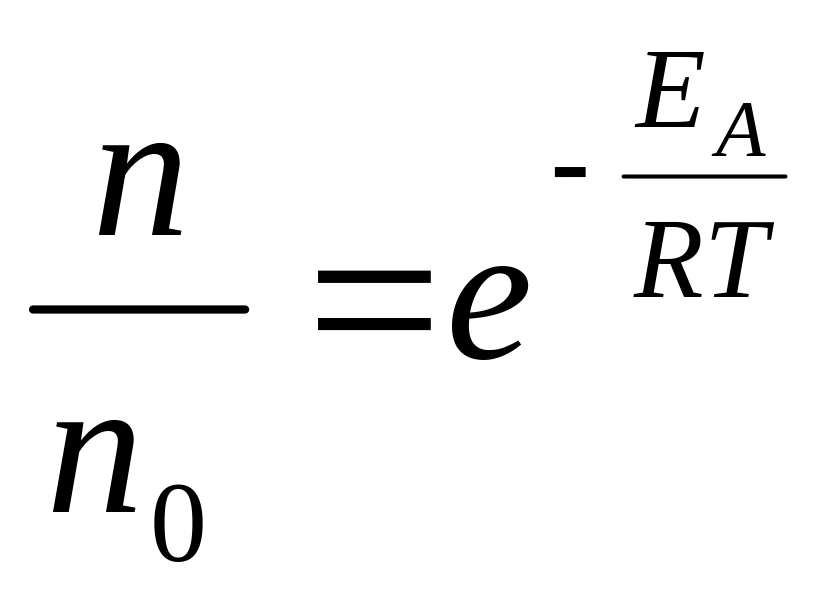
n₀ – количество всех молекул

n – количество тех, которые обладают энергией > E_A.

Если концентрации всех веществ в уравнении (5) были равны 1, то k пропорциональна числу ударений молекул.

, (уравнение Аррениуса)

A – количество соударений между молекулами в единицу времени.

Согласно кинетической теории:

,

,

.

N_A – число Авогадро,

k – постоянная Больцмана.

Вводят поправочный множитель:

, p – стерический множитель.

• Существует теория, согласно которой, молекула ударяется не при каждом соударении, поэтому вводят p, который должен быть p≤1.

• Другая теория, которая может объяснить возникновение p, называется теорией активированного комплекса: между исходным и конечным состоянием существует промежуточное состояние, которое называется активированным комплексом, p определяется энтропией образования активированного комплекса.

, S_A может быть и «+» и «–».

Если S_A>>0, то p>1 (быстрые реакции – быстрее, чем по уравнению Аррениуса)

Если S_A≈0, то p≈1 («нормальные» реакция)

Если S_A<<0, то p<1 («медленные» реакции)

Из уравнения Аррениуса , что скорость химической реакции зависит от температуры.

Влияние температуры на скорость химических реакций определяется уравнением Вант-Гоффа.

, Q₁₀ – коэффициент Вант-Гоффа (равен отношению температур, отличающихся на 10º).

⇒ Если Е_А достаточно высока, то влияние температуры будет заметно, Q₁₀=1,4÷2,5. Если Е_А мало, то Q₁₀ близок к 1.