4. Операции с матрицами

Задание 10

Даны две матрицы:

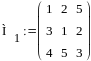
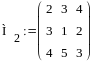
Пользуясь кнопкой «Векторные и матричные операции» панели Математика

найдите:

• сумму; разность; скалярное произведение матриц;

• разность числа 5 и каждого элемента матрицы М₁; числа (-7) и каждого элемента матрицы М₂;

• с

  

  умму числа 12 с элементами матриц М₁ и М₂;

• произведение числа 8 и матрицы М₁; числа 0,4 и матрицы М₂;

• частное матрицы М₁ с числом 3 и матрицы М₂ с числом (-4);

• транспонируйте каждую матрицу (кнопка М^Т );

• найдите определители матриц.

6. Р ешение систем линейных уравнений матричными способами

Системы линейных уравнений в MathCad можно решить разными способами.

Рассмотрим три способа:

• Метод Крамера

• Метод обратной матрицы

• Использование функции lsolve

Задание 11

Дана система линейных уравнений. Решите систему тремя способами.

x + 2y + 3z + 4t = 30

-x + 2y - 3z + 4t = 10

y – z + t = 3

x + y + z + t = 10

1. Метод Крамера

   1. Найдём главный и дополнительные определители матриц, составленных из коэффициентов уравнений.

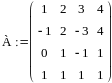
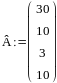
Так как главный определитель отличен от нуля, то система имеет единственное решение.

Найдём это решение, т.е. найдём значения x, y, z, t, которые обращают каждое уравнение системы в верное равенство.

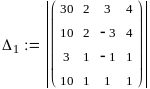
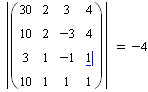
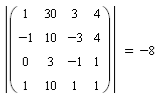
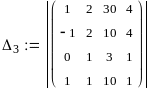
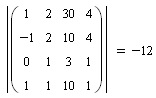
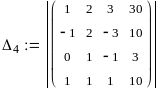
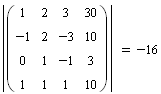
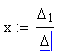
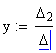
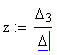
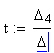
x = 1 y = 2 z = 3 t = 4

Ответ: (1; 2; 3; 4)

2. Метод обратной матрицы

О

бозначим искомое решение через C.

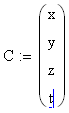
Тогда это решение можно найти по формуле: С= А^-1  В, где А^-1 – это матрица, обратная матрице А, а В – это матрица, составленная из чисел, стоящих в правых частях уравнений системы (смотри предыдущий пример).

1. Запишем матрицы:

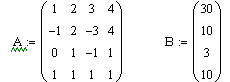
2. Вычислим обратную матрицу.

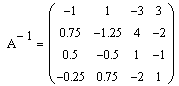
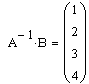
3. Перемножим матрицы А^-1 и В.

Ответ: С = (1, 2 ,3, 4), т.е. x = 1, y = 2, z = 3, t = 4.

4. Использование функции lsolve

Для нахождения решения можно также использовать функцию lsolve

( Меню Вставка Функция)

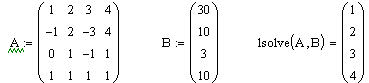
Ответ: (1, 2, 3, 4)

Убедитесь, что ответы, найденные разными способами совпадают.

Задание 12

Даны системы линейных уравнений. Решите каждую систему тремя способами.

x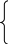 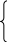+ 2y +3z =7 2x₁ - x₂ + x₃ = 1

x -3y +2z =5 3x₁ + x₂ - 3x₃ = 0

x + y + z =3 x₁ + 3x₂ – 4x₃ = 2