Міністерство освіти і науки України

Національний технічний університет України

"Київський політехнічний інститут"

Кафедра оптичних та оптико-електронних приладів

ПОЯСНЮВАЛЬНА ЗАПИСКА

до курсового проекту

з дисципліни «Теорія оптичних систем»

тема: «Монокуляр з призмою Пехана»

Керівник: Чиж І. Г. Виконав: Лисак І.О.

студент ІІІ курсу

групи ПО-02

залікова книжка

№ ПО-0206

Київ 2013

Зміст

Вступ………………………………………………………………………………...4

1. Огляд схем телескопічних систем, об’єктивів та окулярів……...........5

1. Габаритний розрахунок оптичної системи……………….…..….….….10

2. Вибір окуляра та об’єктива…………………………………..….….…… 15

3. Компоновка оптичної системи …………………..………..….........…....18

4. Абераційний аналіз остаточних аберацій…… …………..….........…...20

Висновок………………………………………………………….…...…..…..…….23

Список використаної літератури………………………..……….………. …….24

Додатки

Додаток 1. Оптичний випуск ……………………………….…………..…..….....32

Додаток 2. Оптична схема ………………………………………………………..33

Додаток 3. Креслення оптичних деталей………………………………...….…...34

Додаток 4. Креслення вузла склейки (об’єктива)…………….……………....….35

Вступ

Призменним монокуляром називається зорова труба Кеплера з приз-менною обертаючою системою. Призмова обертає, система представ-ляє собою:

 

а) одиночну призму, у якої одна з граней виконана у вигляді даху (призми Лемана, Шмідта та ін);

б) систему двох призм (Аббе, Пєха, Порро I-го роду та ін);

в) систему трьох призм (Порро II-го роду та ін.)

У даному курсовому проекті в якості обертаючої системи вико-ється призма Пєхана.

Призмова обертає, система не тільки повертає на 180 площину зображення, що формується об'єктивом зорової труби, але і здійснювала злам або паралельний перенесення оптичної осі.

Призмові обертаючі системи сприяють скороченню осьової довжини зорової труби за рахунок зламів оптичної осі усередині системи.

Інші компоненти монокуляра (об'єктив і окуляр) такі ж, як і в звичайних зорових трубах Кеплера. Об'єктив - як правило, двохлінзових склейка, окуляр виконується за схемами Кельнера, Ерфле, Симетричного оку-ляра, Рамсден, Гюйгенса та ін

Даний курсовий проект присвячений розрахунку оптичної системи Монок-ляра з обертаючою призменной системою. Вихідними даними для розрахунку є найбільш важливі параметри оптичної системи монокуляра такі як: видиме збільшення, осьова довжина оптичної системи, кут поля зору в просторі предметів, діаметр вихідного зіниці, положення вхідного і вихідного зіниць, кутовий межа дозволу, допустимий коефіцієнт виньетирования крайнього похилого пучка променів . У результаті розрахунку необ-хідно отримати дані для розробки креслення оптичної схеми - конст-руктівних параметри і марки скла всіх елементів системи, діаметри і по ложение діафрагм, відстані між елементами.

1. Огляд оптичних схем монокулярів : об'єктивів, обертаючих систем окулярів.

1.1 Огляд схем телескопічної системи

Оптичні системи, призначені для спостереження далеких предметів, називаються телескопічними системами, чи зоровими трубами.

До телескопічних систем відносяться системи геодезичних приладів (теодоліт, нівелір і ін.), астрономічних труб, спостережливих приладів (біноклі, перископи, далекоміри і т.п.) Телескопічні системи працюють разом з оком спостерігача, тому їхній ще називають зоровими трубами.

Тому що розглянутий предмет дуже вилучений, то можна вважати, що промені, що виходять з будь-якої крапки предмета, входять у телескопічну систему рівнобіжними пучками. Для того щоб око спостерігача без акомодації бачив різкий зображення предмета, необхідно, щоб з телескопічної системи виходили також рівнобіжні пучки променів.

Отже, принцип дії телескопічної системи полягає в тому, що, якщо від двох крапок вилученого предмета в неї надходять два пучки рівнобіжних променів і кут між пучками дорівнює ω, те на виході телескопічної системи промені залишаються рівнобіжними, але кут між пучками зміниться і буде дорівнює ω (мал. 1.1). Якщо ω > ω^’, те око спостерігача побачить зображення предмета під великим кутом зору, тобто предмет буде здаватися наближеним до спостерігача.

Рис. 1.1. Принцип дії телескопічної системи

Телескопічна система, як мінімум, повинна складатися з двох компонентів — об'єктива й окуляра. Щоб рівнобіжні промені пучків у просторі предметів були рівнобіжними й у просторі зображень, необхідно сполучити задній фокус об'єктива з переднім фокусом окуляра, при цьому оптичний інтервал ∆ буде дорівнює нулю.

Основними оптичними характеристиками телескопічної системи є збільшення Г_т, кутове поле 2ω, діаметр вихідної зіниці D’, видалення вихідної зіниці від останньої поверхні окуляра S’_p’ і здатність, що дозволяє ?

Прості телескопічні системи складаються з двох компонентів: об'єктива й окуляра.

1.1.1 Зорова труба Кеплера.

Зорова труба Кеплера (мал. 1.2). Ця система має позитивний об'єктив і позитивний окуляр. Тому що фокусні відстані об'єктива f’_об і окуляра f'ок-величины позитивні, збільшення труби Кеплера негативне (Г_т<0), тобто вона дає цілком перевернене зображення. У площині дійсного зображення, що дається об'єктивом, установлена польова діафрагма D_п. У цій же площині поміщають пластинку з перекрестием чи шкалою, що називають сіткою. Повертаючи зорову трубу, її можна навести на будь-яку крапку простору предметів і по сітці показаний хід променів у трубі Кеплера з окуляром Кельнера. Визначимо положення зіниць. Матеріальними діафрагмами є: оправа об'єктива D₁ польова діафрагма D_пд, оправа першої лінзи окуляра D₂ і оправа другої лінзи окуляра D₃.

Знайдемо в зворотному ході зображення всіх діафрагм у просторі предметів. Зображення оправи об'єктива збігається із самою оправою, тому що пере нею немає фокусирующих елементів; зображення польової діафрагми об'єктивом буде в нескінченності, тобто збігається з площиною предметів, що спостерігаються. Тому що ця оправа розташована близько до фокальної площини об'єктива, те її зображення виходить на великій відстані перед об'єктива і буде значно збільшеним. Оправу другої лінзи окуляра спочатку зобразимо

через першу лінзу — це проміжне зображення виходить трохи збільшеним праворуч від першої лінзи (мниме), оскільки f’ першої лінзи майже в 2 рази більше відстані між лінзами окуляра.

Рис. 1.2. Оптична схема сурми Кеплера

Вважаючи проміжне зображення предметом для об'єктива, знайдемо його зображення. Тому що «предмет» знаходиться від об'єктива на відстані, більшому f’_об, але меншому 2 f’_об, те збільшене його зображення буде знаходитися перед об'єктивом на відстані, більшій подвійної фокусної відстані об'єктива. Перетин пучка променів, що йдуть з нескінченно вилученої крапки предмета, обмежується оправою об'єктива, отже, вона і є вхідною зіницею D і одночасно апертурною діафрагмою, а її зображення D’₁, що дається окуляром, — вихідною зіницею D’, з яким сполучається зіниця ока спостерігача. Якщо зіниця ока D_гл менше вихідної зіниці зорової труби, то ефективний діаметр вхідної зіниці зменшується в D’/ D_гл раз.

Простота конструкції, відсутність він’єтування при порівняно великих збільшеннях і кутовому полі, наявність площини дійсного зображення, де можна помістити сітку, є перевагами труби Кеплера. Істотний недолік її — перевернене зображення, тому трубу Кеплера застосовують у тих випадках, коли розглянутий предмет може бути сам перевернуть, наприклад, геодезична рейка, оцифровка якої робиться в переверненому виді.

Трубу Кеплера застосовують також в астрономічних інструментах, де наявність переверненого зображення не заважає спостереженню за зоряним небом.

1.1.2 Зорова труба Галілея.

Зорова труба Галилея. На відміну від труби Кеплера зорова труба Галилея має негативний окуляр. Як окуляр найчастіше використовують просту двоввігнуту лінзу, передній фокус якої сполучений із заднім фокусом об'єктива. Тому що в трубі Галилея f’_об > 0, а f’_ок < 0, те її збільшення позитивне Г_т>0, отже, зображення пряме. Довжину оптичної системи L_c з нескінченно тонких компонентів, як і труби Кеплера, визначають по формулі L_c = f’_об + f’_ок .Тому що для труби Галилея f’_ок < 0, те її довжина буде менше фокусної відстані об'єктива (мал. 1.3). При тому самому збільшенні і рівних фокусних відстанях об'єктивів система Галилея коротше системи Кеплера на дві фокусних відстані окуляра. Незважаючи на такі позитивні властивості, як пряме зображення і мала довжина, труба Галилея має обмежене застосування.

Рис. 1.3. Оптична схема сурми Галілея

1.2 Огляд об’єктивів монокулярів.

Об'єктив телескопічної системи служить для одержання дійсного проміжного зображення. Основні характеристики об'єктива: фокусна відстань f’_об, відносний отвір D/f’_об, кутове поле 2ω, що дозволяє здатність ψ і якість зображення (стан корекції).

У більшості випадків об'єктиви телескопічних систем мають порівняно великі фокусні відстані. Чим більше фокусна відстань об'єктива, а отже, і збільшення телескопічної системи, де встановлений такий об'єктив, тим менше його кутове поле.

Рис. 2.1. Об'єктиви телескопічних систем:

а – двохлінзовий; б – із двох несклеєнних лінз; у – трьохлінзові; м – чотирьохлінзові

Найбільш розповсюдженим є двухлинзовый склеєний об'єктив (мал. 2.1, а), одна з лінз якого позитивна (із крона), друга негативна (із флінта). Комбінуючи скла різних марок, вдається одержати об'єктив з гарним виправленням аберацій у центрі полючи при відносному отворі 1:5. Кутове поле двухлинзового об'єктива не перевищує 8—10°. Чим вище вимоги до якості зображення, тим менше відносний отвір і кутове поле об'єктива. Наприклад, в астрономічних трубах і коллиматорах, де потрібно особливо гарна якість зображення, застосовують двухлинзовые об'єктиви з відносним отвором від 1:10 до 1:12 з кутовим полем 1—2°.

В об'єктиві з двох несклеєних лінз (мал. 2.1, б) відносний отвір може бути підвищене до 1:3.

Крім того, за рахунок зміни зазору між лінзами можна в невеликих межах змінювати фокусна відстань і в такий спосіб одержувати точно задана фокусна відстань, об'єктива, не витримуючи твердих допусків на виготовлення лінз.

При великому відносному отворі від 1:1,5 до 1:2 застосовують трехлинзовые об'єктиви (мал. 2.1, в), кутове поле яких також невелико і складає 10—12°. Якщо об'єктив повинний мати велике поле, то використовують більш складні конструкції, наприклад, четырехлинзовые. Іноді в якості четырехлинзового широкоугольного об'єктива застосовують конструкцію типу окуляра, що складає з двох однакових склеєних компонентів (мал. 2.1, г). Вхідна зіниця в такого об'єктива завжди винесений уперед. Відносний отвір його 1:4, кутове поле до 40°.

1.3 Окуляри телескопічних систем.

Основні характеристики окулярів: фокусна відстань f’_ок видиме збільшення Г, відносний чи отвір діаметр вихідної зіниці D', кутове поле 2ω', видалення вихідної зіниці від останньої поверхні S'_р', передній фокальний відрізок S_F.

Окуляри звичайно мають позитивна задня фокусна відстань, за винятком окуляра труби Галилея. Для фокусних відстаней окулярів установлений нормальний ряд значень: 10, 15, 20, 25, 30, 35, 40 і 50 мм. Найбільше поширення мають окуляри з фокусною відстанню від 20 до 30 мм.

Окуляри розраховують для нормального (эмметропического) ока; у цьому випадку зображення, отримане об'єктивом, знаходиться в передній фокальній площині окуляра. Таке положення окуляра будемо називати нульовим. Для аметропического ока окуляр переміщають від нульового положення: убік до об'єктива (усувають) для короткозорого ока і від об'єктива (висувають) для далекозорого.

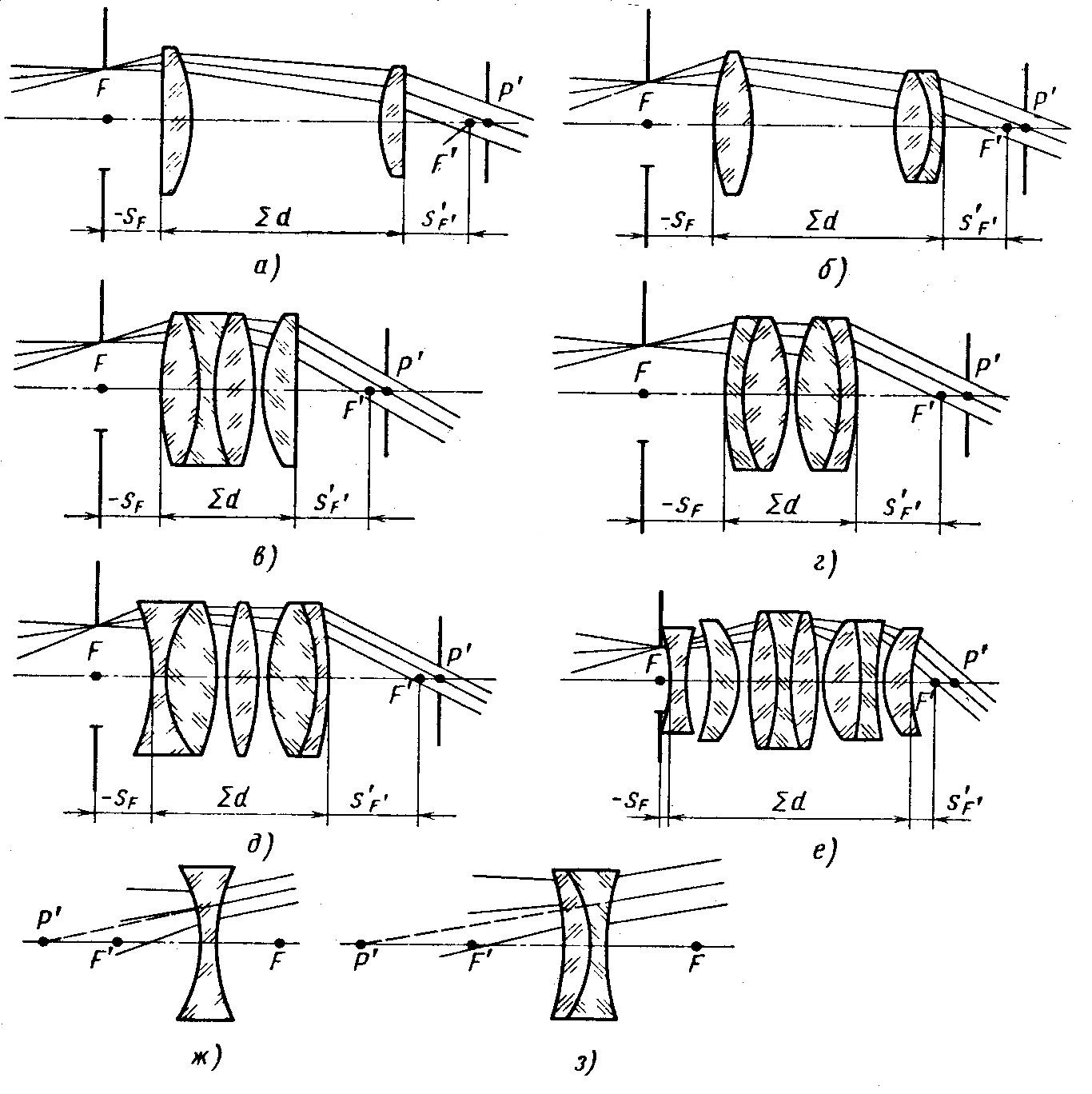
Рис. 3.1. Окуляри телескопічних систем:

а – Рамсдена; б – Кельнера; у – отоскопічний; м – симетричнний; д – Ерфле; е – ширококутовий; ж, з – від’ємні