Лабораторная работа №4 Графика и визуализация данных
1
Построить графики функций одной переменной на указанных интервалах. Вывести Графики различными способами:
В отдельные графические окна
В одно окно на одни оси
Дать заголовки, разместить подписи к осям. Легенду, использовать различные цвета, стили линий и типы маркеров, нанести сетку.
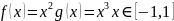
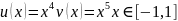
x=[-1,1]
x =
-1 1
h=(1+1)/10
h =
0.2000
x1=[-1:0.2:1]
x1 =
-1.0000 -0.8000 -0.6000 -0.4000 -0.2000 0 0.2000 0.4000 0.6000 0.8000 1.0000
f=x1.^2
f =
1.0000 0.6400 0.3600 0.1600 0.0400 0 0.0400 0.1600 0.3600 0.6400 1.0000
g=x1.^3
g =
-1.0000 -0.5120 -0.2160 -0.0640 -0.0080 0 0.0080 0.0640 0.2160 0.5120 1.0000
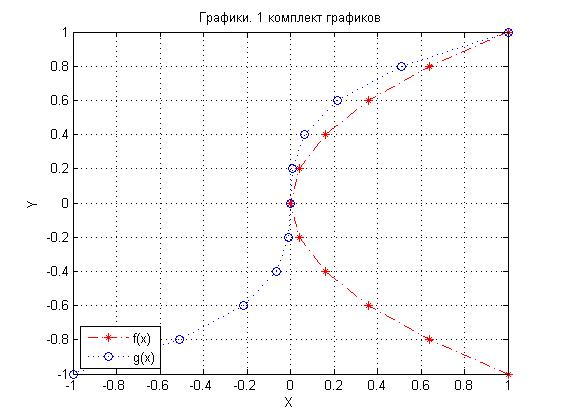
plot(f,x1,'m*-.')
plot(g,x1,'go:')
plot(f,x1,'r*-.',g,x1,'bo:')
plot(f,x1,'r*-.',g,x1,'bo:'); title('Графики. 1 комплект графиков'); grid on; legend('f(x)','g(x)',3); xlabel('X'); ylabel('Y')
X=[-1,1]
X =
-1 1
h=(1+1)/10
h =
0.2000
x2=[-1:0.2:1]
x2 =
-1.0000 -0.8000 -0.6000 -0.4000 -0.2000 0 0.2000 0.4000 0.6000 0.8000 1.0000
u=x2.^4
u =
1.0000 0.4096 0.1296 0.0256 0.0016 0 0.0016 0.0256 0.1296 0.4096 1.0000
v=x2.^5
v =
-1.0000 -0.3277 -0.0778 -0.0102 -0.0003 0 0.0003 0.0102 0.0778 0.3277 1.0000
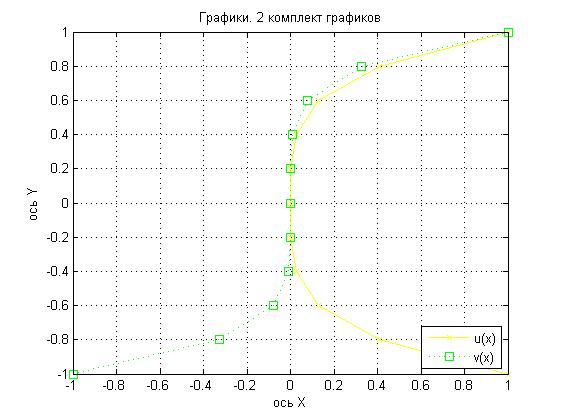
plot(u,x2,'yx-')
plot(v,x2,'gs:')
plot(u,x2,'yx-',v,x2,'gs:'); title('Графики. 2 комплект графиков');grid on; legend('u(x)','v(x)',4); xlabel('ось X'); ylabel('ось Y')
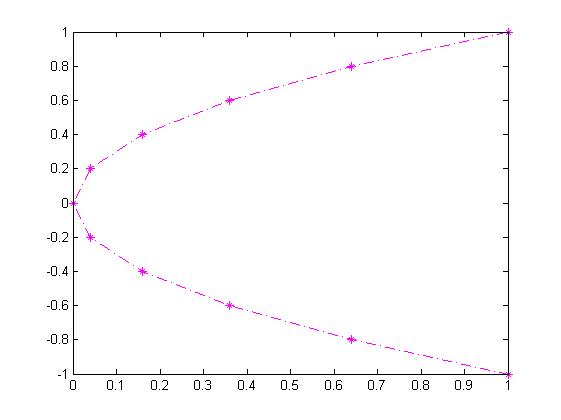
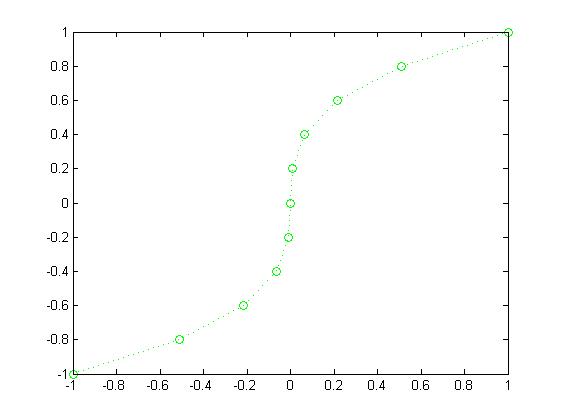
f(x) g(x)
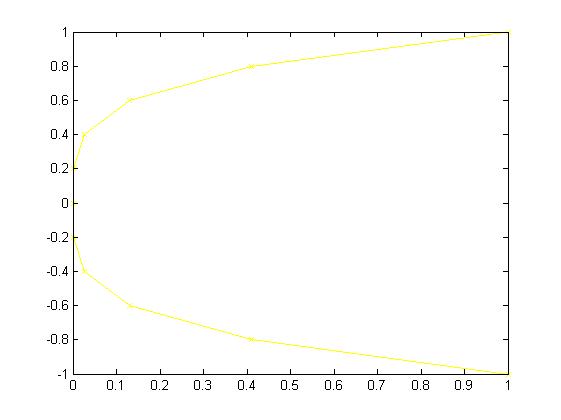
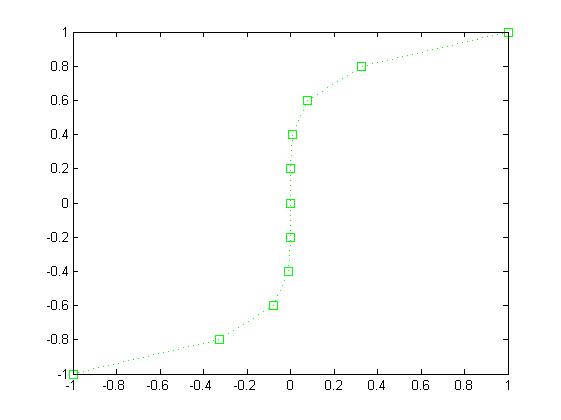
u(x) v(x)
2
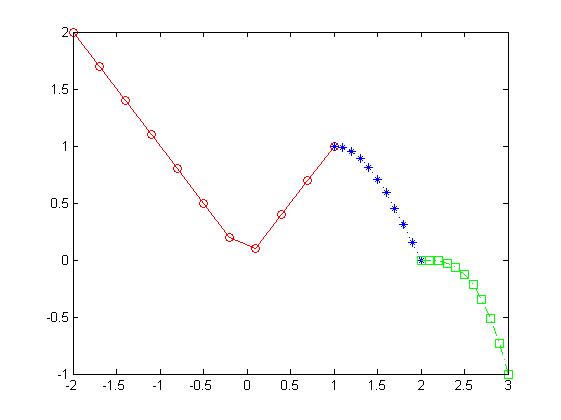
Построить график кусочно-заданной функции, отобразить ветви разными маркерами и цветами:
x1=-2:0.3:1
x1 =
-2.0000 -1.7000 -1.4000 -1.1000 -0.8000 -0.5000 -0.2000 0.1000 0.4000 0.7000 1.0000
f1=abs(x1)
f1 =
2.0000 1.7000 1.4000 1.1000 0.8000 0.5000 0.2000 0.1000 0.4000 0.7000 1.0000
x2=1:0.1:2
x2 =
1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000
f2=sin((pi./2).*x2)
f2 =
1.0000 0.9877 0.9511 0.8910 0.8090 0.7071 0.5878 0.4540 0.3090 0.1564 0.0000
x3=2:0.1:3
x3 =
2.0000 2.1000 2.2000 2.3000 2.4000 2.5000 2.6000 2.7000 2.8000 2.9000 3.0000
f3=(2-x3).^3
f3 =
0 -0.0010 -0.0080 -0.0270 -0.0640 -0.1250 -0.2160 -0.3430 -0.5120 -0.7290 -1.0000
plot(x1,f1,'ro-',x2,f2,'b*:',x3,f3,'gs-.')
3
Построить график параметрически заданной функции, используя plot и comet.
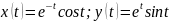
t=0:pi/20:2*pi
t =
Columns 1 through 12
0 0.1571 0.3142 0.4712 0.6283 0.7854 0.9425 1.0996 1.2566 1.4137 1.5708 1.7279
Columns 13 through 24
1.8850 2.0420 2.1991 2.3562 2.5133 2.6704 2.8274 2.9845 3.1416 3.2987 3.4558 3.6128
Columns 25 through 36
3.7699 3.9270 4.0841 4.2412 4.3982 4.5553 4.7124 4.8695 5.0265 5.1836 5.3407 5.4978
Columns 37 through 41
5.6549 5.8119 5.9690 6.1261 6.2832
x=exp(-t).*cos(t)
x =
Columns 1 through 12
1.0000 0.8441 0.6947 0.5562 0.4316 0.3224 0.2290 0.1512 0.0879 0.0381 0.0000 -0.0278
Columns 13 through 24
-0.0469 -0.0589 -0.0652 -0.0670 -0.0655 -0.0617 -0.0563 -0.0499 -0.0432 -0.0365 -0.0300 -0.0240
Columns 25 through 36
-0.0187 -0.0139 -0.0099 -0.0065 -0.0038 -0.0016 -0.0000 0.0012 0.0020 0.0025 0.0028 0.0029
Columns 37 through 41
0.0028 0.0027 0.0024 0.0022 0.0019
y=exp(t).*sin(t)
y =
Columns 1 through 12
0 0.1830 0.4231 0.7273 1.1018 1.5509 2.0762 2.6755 3.3416 4.0606 4.8105 5.5594
Columns 13 through 24
6.2637 6.8663 7.2949 7.4605 7.2564 6.5579 5.2230 3.0938 0.0000 -4.2357 -9.7903 -16.8298
Columns 25 through 36
-25.4959 -35.8885 -48.0449 -61.9140 -77.3274 -93.9649 -111.3178 -128.6481 -144.9468 -158.8919 -168.8097 -172.6409
Columns 37 through 41
-167.9176 -151.7550 -120.8641 -71.5923 -0.0000
plot(x,y,'b*-')
comet(x,y)
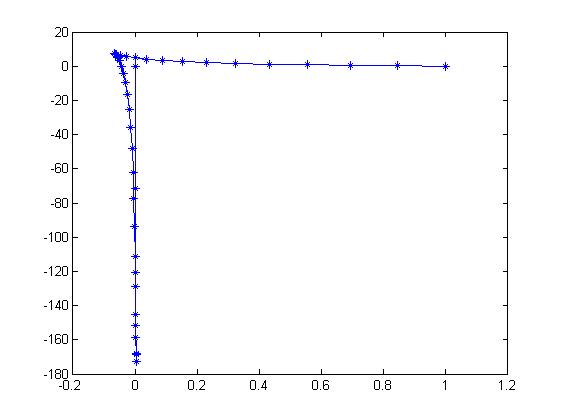
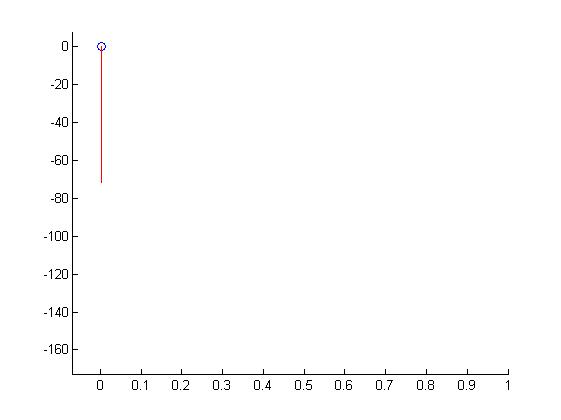
plot comet
4
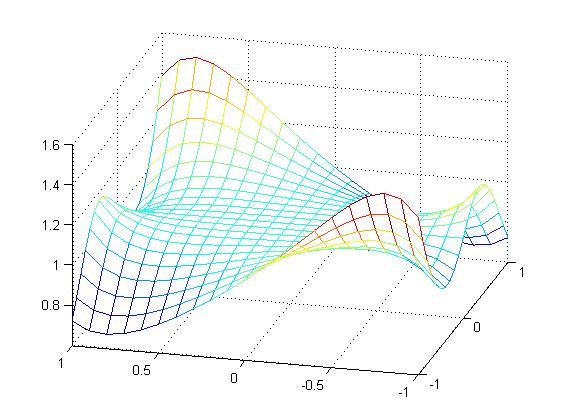
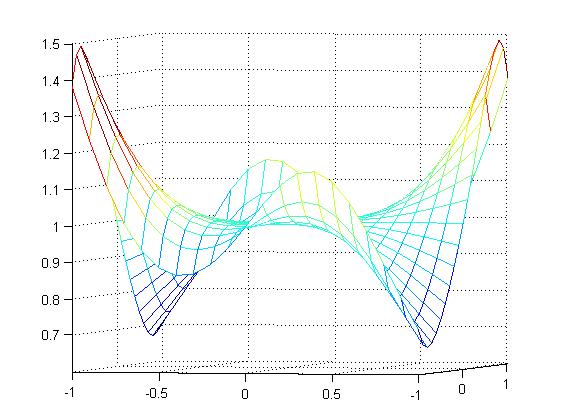
Визуализировать функцию двух переменных на прямоугольной области определения различными способами:
Каркасной поверхностью;
Залитой цветом каркасной поверхностью;
Промаркированными линиями уровня;
Освещённой поверхностью.
Расположить графики в отдельных графических окнах. Представить вид каркасной или освещённой поверхности с нескольких точек обзора.
[X,Y]=meshgrid(-1:0.1:1,-1:0.1:1)
X =…
Y =…
Z=(sin(X.^2)+cos(Y.^2)).^(X.*Y)
Z =…
mesh(X,Y,Z)
surf(X,Y,Z)
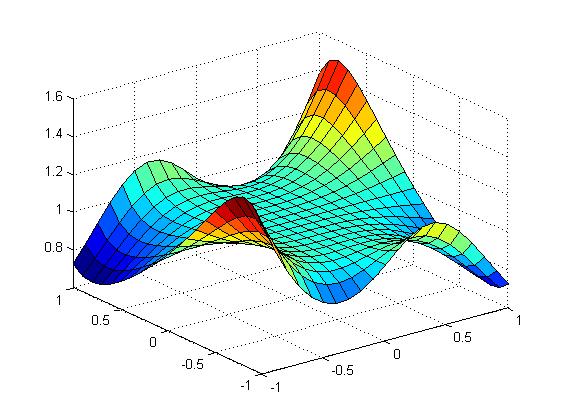
meshc(X,Y,Z)
surfl(X,Y,Z)
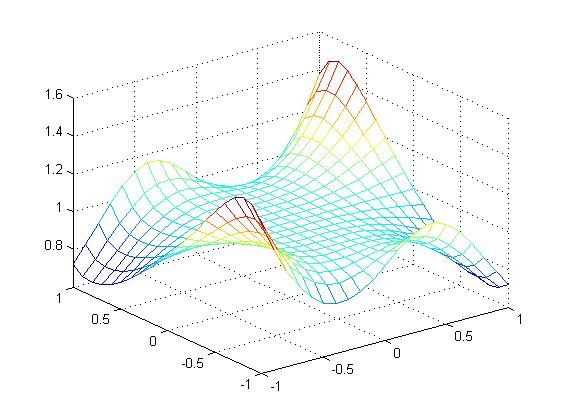
mesh surf
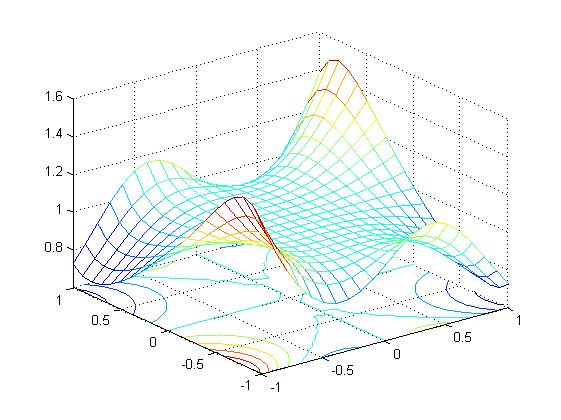
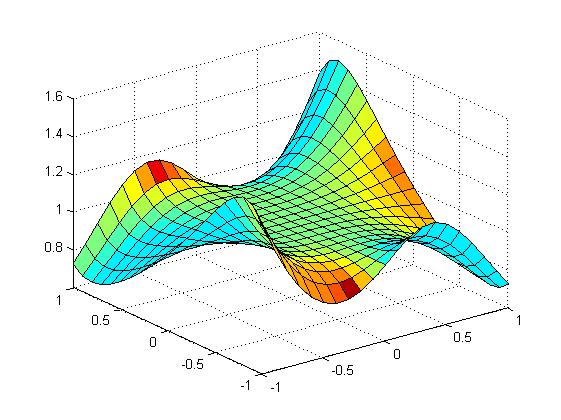
meshc surfl
