Оглавление

Информационный пакет MatLAB 4

Лабораторная работа №1 5

ВЫЧИСЛЕНИЕ АРИФМЕТИЧЕСКИХ ВЫРАЖЕНИЙ 5

Лабораторная работа №2 6

Вектор-строки и вектор-столбцы 6

1 6

2 8

Лабораторная №3 9

Матрицы 9

1 9

2 10

3 12

4 14

Лабораторная работа №4 16

Графика и визуализация данных 16

1 16

2 18

3 19

4 20

Лабораторная работа №5 22

Файл-функции и файл-программы 22

1 22

2 22

Лабораторная работа №6 23

Програмирование 23

1 23

2 24

Лабораторная работа №7 25

Работа со строками 25

Лабораторная работа №8 26

Массивы структур и массивы ячеек 26

Лабораторная работа №9 27

Текстовые файлы 27

1 27

2 28

Лабораторная работа №10 29

Программирование циклических процессов с неизвестным числом повторений 29

Лабораторная работа №11 30

Решение нелинейного уравнения методом половинного деления и с помощью функйии fzero. Сравнить результаты. 30

Лабораторная работа №12 32

Вычисление определённого интеграла с помощью квадратурных формул средних прямоугольников, трапеций с помощью встроенных функций trap и quard. Сравнить результаты. 32

Информационный пакет MatLab

Язык MATLAB является высокоуровневым языком программирования, включающим основанные на матрицах структуры данных, широкий спектр функций, интегрированную среду разработки, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования.

Программы, написанные на MATLAB, бывают двух типов — функции и скрипты. Функции имеют входные и выходные аргументы, а также собственное рабочее пространство для хранения промежуточных результатов вычислений и переменных. Скрипты же используют общее рабочее пространство. Как скрипты, так и функции не интерпретируются в машинный код и сохраняются в виде текстовых файлов. Существует также возможность сохранять так называемые pre-parsed программы — функции и скрипты, обработанные в вид, удобный для машинного исполнения. В общем случае такие программы выполняются быстрее обычных.

Основной особенностью языка MATLAB является его широкие возможности по работе с матрицами, которые создатели языка выразили в лозунге думай векторно (англ. Think vectorized).

Ключевые особенности

• Платформонезависимый высокоуровневый язык программирования ориентированный на матричные вычисления и разработку алгоритмов

• Интерактивная среда для разработки кода, управления файлами и данными

• Функции линейной алгебры, статистики, анализ Фурье, решение дифференциальных уравнений и др.

• Богатые средства визуализации, 2-D и 3-D графика.

• Встроенные средства разработки пользовательского интерфейса для создания законченных приложений на MATLAB

• Средства интеграции с C/C++, наследование кода, ActiveX технологии  

Лабораторная работа №1 вычисление арифметических выражений

Требуется занести в некоторую переменную значения выражений при заданных х=-1,75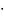 10^-3 и у=3,1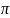 , отобразить результат и изучить информацию о переменных при помощи команды whos. (Просмотр текущих переменных рабочей среды производиться при помощи команды whos).

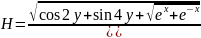
LAB 1

x=-1.75*(10^(-3))

x =

-0.0018

y=3.1*pi

y =

9.7389

H=(sqrt(cos(2*y)+sin(4*y)+sqrt(exp(x)+exp(-x))))/(((exp(x)+exp(x))^(1/3))* (sin(4*y)+cos(2*y)-2)^2)

H =

24.5654

whos x y

Name Size Bytes Class Attributes

x 1x1 8 double

y 1x1 8 double

Лабораторная работа №2 Вектор-строки и вектор-столбцы

1

Для заданных векторов и a и b длины п:

1. Вычислить их сумму, разность и скалярное произведение;

2. Образовать вектор с=[a₁, a₂, … , a_n, b₁, b₂, … , b_n], определить его максимальный и минимальный элементы и поменять их местами;

3. Упорядочить вектор с по возрастанию и убыванию;

4. Переставить элементы вектора с в обратном порядке и записать результат в новый вектор;

5. Найти векторное произведение u=[a1, a3, a4] и v=[b2, b3, b4].

a=[5.3 6.8 -7.1 6.8 -4.0 -2.3 -4.4 -0.2] b=[7.5 -1.5 -4.9 -4.6 -2.3 -5.3 5.5 2.3]

u=[5.3,-7.1,6.8] v=[-1.5,-4.9,-4.6]

a=[5.3 6.8 -7.1 6.8 -4.0 -2.3 -4.4 -0.2]

a =

5.3000 6.8000 -7.1000 6.8000 -4.0000 -2.3000 -4.4000 -0.2000

b=[7.5 -1.5 -4.9 -4.6 -2.3 -5.3 5.5 2.3]

b =

7.5000 -1.5000 -4.9000 -4.6000 -2.3000 -5.3000 5.5000 2.3000

c=a+b

c =

12.8000 5.3000 -12.0000 2.2000 -6.3000 -7.6000 1.1000 2.1000

d=a-b

d =

-2.2000 8.3000 -2.2000 11.4000 -1.7000 3.0000 -9.9000 -2.5000

e=dot(a,b)

e =

29.7900

C=[5.3 6.8 -7.1 6.8 -4.0 -2.3 -4.4 -0.2 7.5 -1.5 -4.9 -4.6 -2.3 -5.3 5.5 2.3]

C =

Columns 1 through 12

5.3000 6.8000 -7.1000 6.8000 -4.0000 -2.3000 -4.4000 -0.2000 7.5000 -1.5000 -4.9000 -4.6000

Columns 13 through 16

-2.3000 -5.3000 5.5000 2.3000

M=max(C)

M =

7.5000

m=min(C)

m =

-7.1000

K=[M m]

K =

7.5000 -7.1000

L=sort(K)

L =

-7.1000 7.5000

C1=sort(C)

C1 =

Columns 1 through 12

-7.1000 -5.3000 -4.9000 -4.6000 -4.4000 -4.0000 -2.3000 -2.3000 -1.5000 -0.2000 2.3000 5.3000

Columns 13 through 16

5.5000 6.8000 6.8000 7.5000

C3=-sort(-C1)

C3 =

Columns 1 through 12

7.5000 6.8000 6.8000 5.5000 5.3000 2.3000 -0.2000 -1.5000 -2.3000 -2.3000 -4.0000 -4.4000

Columns 13 through 16

-4.6000 -4.9000 -5.3000 -7.1000

Cnew=C(16:-1:1)

Cnew =

Columns 1 through 12

2.3000 5.5000 -5.3000 -2.3000 -4.6000 -4.9000 -1.5000 7.5000 -0.2000 -4.4000 -2.3000 -4.0000

Columns 13 through 16

6.8000 -7.1000 6.8000 5.3000

u=[5.3,-7.1,6.8]

u =

5.3000 -7.1000 6.8000

v=[-1.5,-4.9,-4.6]

v =

-1.5000 -4.9000 -4.6000

V=cross(u,v)

V =

65.9800 14.1800 -36.6200

2

Вычислить значения функции на отрезке в заданном числе N равномерно отстоящих друг от друга точек.

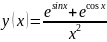
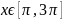
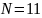
x=[pi, 3*pi]

x =

3.1416 9.4248

h=(9.4248-3.1416)/11

h =

0.5712

x1=[3.1416:0.5712:9.4248]

x1 =

3.1416 3.7128 4.2840 4.8552 5.4264 5.9976 6.5688 7.1400 7.7112 8.2824 8.8536 9.4248

y=(exp(sin(x1))+exp(cos(x1)))./(x1.^2)

y =

0.1386 0.0735 0.0579 0.0647 0.0813 0.0935 0.0912 0.0795 0.0646 0.0458 0.0274 0.0154

y=(exp(sin(x))+exp(cos(x)))./(x.^2)

y =

0.1386 0.0154