3.5. Циркуляция вектора индукции магнитного поля в вакууме

Аналогично циркуляции вектора напряженности электростатического поля в магнитном поле вводится понятие циркуляции вектора магнитной индукции по заданному замкнутому контуру:

где - вектор элементарной длины контура, направленный вдоль обхода контура; - составляющая вектора в направлении к касательной к контуру с учетом выбранного обхода контура; - угол между векторами и .

Теорема о циркуляции вектора или закон полного тока для магнитного поля в вакууме формулируется следующим образом: циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром, т.е.

(3.19)

где n – число проводников с токами, охватываемых контуром l произвольной формы.

К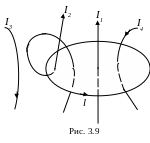 аждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода контура правилом правого винта; ток противоположного направления считается отрицательным. Например, для системы токов, охваченных контуром l на рис. 3.9, закон полного тока запишется следующим образом:

Выражение (3.19) справедливо только для магнитного поля в вакууме, так как для поля в веществе необходимо дополнительно учитывать молекулярные токи (микротоки).

Убедимся в справедливости теоремы о циркуляции вектора на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного «к нам» (рис. 3.10).

Представим себе замкнутый контур l в виде окружности радиуса r. В каждой точке этой окружности вектор одинаков по модулю и направлен п о касательной к ней. Следовательно, в данном случае циркуляция вектора будет равна

Согласно выражению (3.19) получим:

или

что полностью согласуется с выражением для индукции магнитного поля прямого тока, выведенным на основе закона Био-Савара-Лапласа.

Сравнивая выражения и для циркуляции векторов и , видно, что между ними существует принципиальное различие: циркуляция вектора напряженности электростатического поля всегда равна нулю, т.е. такое поле является потенциальным; циркуляция вектора отлична от нуля, поэтому магнитное поле является вихревым.

Теорема о циркуляции вектора позволяет находить магнитную индукцию поля без применения закона Био-Савара-Лапласа.

3.6. Теорема Гаусса для магнитного поля в вакууме

Потоком вектора магнитной индукции или магнитным потоком сквозь малую поверхность площадью dS называется скалярная физическая величина, равная

(3.20)

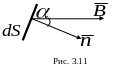г де - проекция вектора на направление нормали к площадке dS (рис. 3.11); - вектор, модуль которого равен dS, а направление совпадает с направлением нормали к площадке.

Магнитный поток сквозь произвольную поверхность площадью S равен

(3.21)

Если магнитное поле однородно, а поверхность плоская, то как частный случай

(3.22)

Если плоская поверхность расположена перпендикулярно вектору , то угол и

Отсюда определяется единица магнитного потока вебер (Вб): 1 Вб – это магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл, т.е.

1 Вб = 1 Тл·м².

Теорема Гаусса для магнитного поля формулируется следующим образом: поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю:

(3.23)

Эта теорема отражает тот факт, что в природе не существует магнитных масс (магнитных зарядов) – источников магнитного поля, на которых начинались бы или заканчивались линии магнитной индукции. Вследствие этого силовые линии магнитного поля не имеют ни начала, ни конца и являются замкнутыми.

Итак, потоки векторов и сквозь замкнутую поверхность в вихревом и потенциальном полях имеют различные выражения:

Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потокосцеплением этого контура. Например, потокосцепление катушки, состоящей из N витков, магнитные потоки через которые одинаковы и равны Ф, определяется как

Потокосцепление контура, обусловленное магнитным полем тока в самом этом контуре, называется потокосцеплением самоиндукции. Потокосцепление контура, обусловленное магнитным полем тока, идущим в другом контуре, называется потокосцеплением взаимной индукции этих двух контуров.

В качестве примера найдем потокосцепление самоиндукции соленоида:

где - магнитный поток через один виток соленоида площадью S.