Вопросы для самоконтроля и повторения

1. Что понимают под электрическим током? Каковы условия возникновения и поддержания электрического тока проводимости?

2. Что называют силой тока, плотностью тока? Каковы их единицы?

3. Какова физическая природа электрического сопротивления проводника? От чего зависит сопротивление металлического проводника?

4. Какова связь между сопротивлением и проводимостью, удельным сопротивлением и удельной проводимостью? Каковы их единицы?

5. Какой участок электрической цепи называют однородным, неоднородным? Выведите закон Ома в дифференциальной форме.

6. Какова физическая сущность ЭДС источника тока, разности потенциалов, напряжения?

7. Как определяется эквивалентное сопротивление проводников при их последовательном и параллельном соединении?

8. Сформулируйте закон Ома в интегральной форме. Какие частные законы можно из него получить?

9. Что называют мощностью электрического тока? Сформулируйте закон Джоуля-Ленца.

10. Выведите закон Джоуля-Ленца в дифференциальной форме. Что называют удельной тепловой мощностью тока?

11. Сформулируйте правила Кирхгофа и запишите их математические выражения.

12. Изложите сущность метода расчета разветвленной электрической цепи с использованием правил Кирхгофа.

Примеры решения задач

З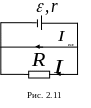 адача 1. Определить ток короткого замыкания источника ЭДС, если при внешнем сопротивлении ток в цепи 0,2 А, а при ток 0,1 А (рис. 2.11).

Дано: , .

Найти:

Решение

По закону Ома для замкнутой цепи

В режиме короткого замыкания источника тока

так как сопротивление закоротки бесконечно мало.

Используя данные для нормальных режимов цепи, получим систему уравнений

откуда

Тогда искомый ток короткого замыкания источника

Ответ:

Задача 2. В схеме на рис. 2.12 перед замыканием ключа К конденсатор емкостью С не был заряжен. Ключ замыкают на некоторое время, в течение которого конденсатор зарядился до напряжения U. Какое количество теплоты выделится к этому моменту времени на резисторе сопротивлением R? ЭДС источника , его внутреннее сопротивление r.

Дано:

Найти:

Решение

По закону сохранения энергии

где энергия источника тока.

С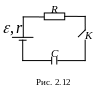 огласно закону Джоуля-Ленца тогда откуда Следовательно,

откуда, учитывая, что получим:

Ответ:

Задача 3. При заданных параметрах цепи, схема которой изображена на рис. 2.13, определить токи во всех ветвях. Внутренними сопротивлениями источников пренебречь.

Д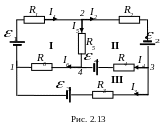 ано:

Найти:

Решение

Выберем направления токов в ветвях, как они показаны на рис. 2.13, и условимся обходить контуры I-III по часовой стрелке.

Составим уравнения по правилам Кирхгофа (всего шесть уравнений):

- по первому правилу Кирхгофа для узлов 1, 2 и 3 соответственно

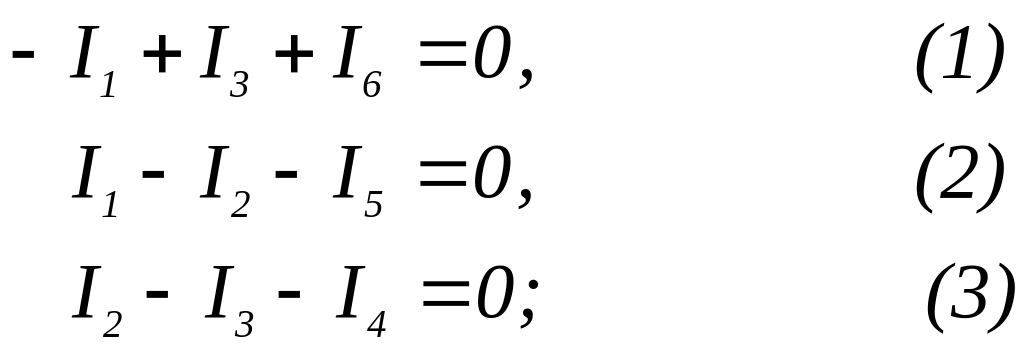
- по второму правилу Кирхгофа для контуров I, II и III имеем:

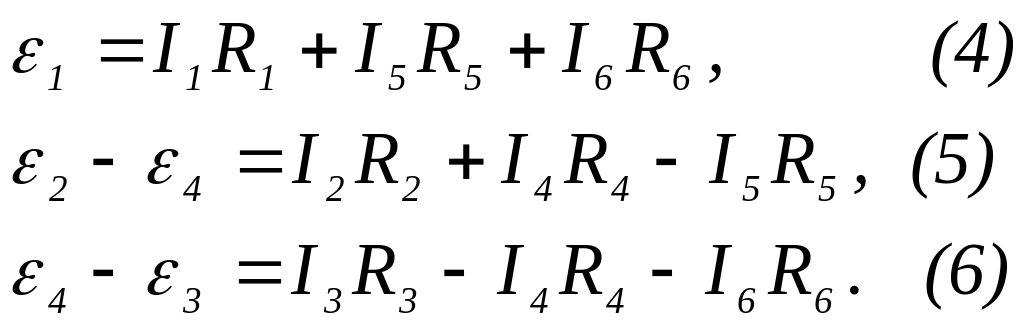
Из уравнений (4)-(6) выразим токи и, подставив их в формулы (1)-(3), с учетом заданных числовых значений получим систему уравнений с тремя неизвестными:

Эту систему можно решить обычными приемами линейной алгебры (методом Гаусса, по формулам Крамера и др.). Воспользовавшись формулами Крамера, найдем:

Из формул (4)-(6) определяем недостающие токи:

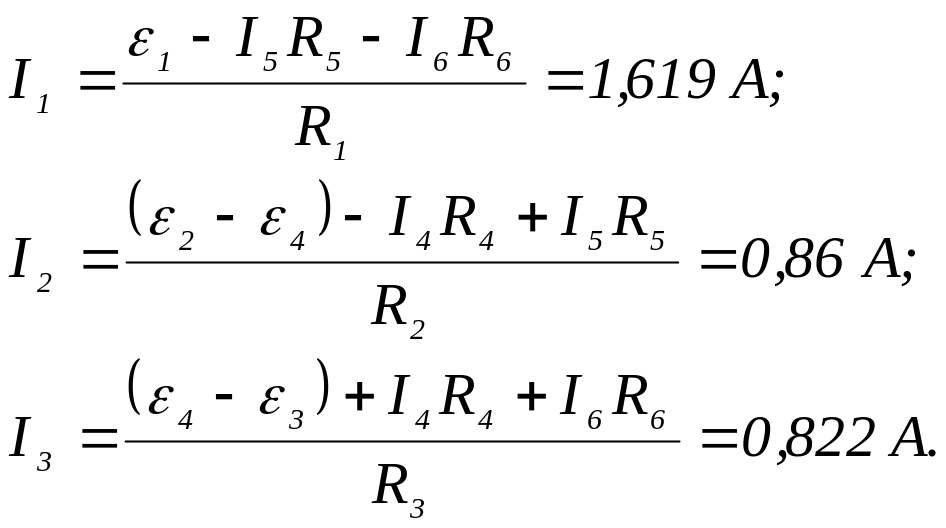
Для проверки расчета составим баланс мощностей в схеме: алгебраическая сумма мощностей источников тока равна сумме мощностей, рассеиваемых в ветвях, т.е.

Для данной задачи левая часть баланса:

правая часть баланса:

Баланс мощностей в цепи выполняется, следовательно, расчет токов в ветвях выполнен верно.

Ответ:

.