2.3.2Расчет прочности ригеля по сечениям наклонным к продольной оси элемента при действии поперечной силы

Расчет ригеля по сечению наклонному к продольной оси элемента выполняется на полную эксплуатационную нагрузку. Расчетная схема ригеля приведена на рисунке 4.5. Значение интенсивности нагрузки q и расчетной длины l₀ точно такие же как и в расчете ригеля по нормальному сечению (смотри п. 2.3.1).

Рисунок 2.3.5 – Расчетная схема ригеля по сечению наклонному к продольной оси элемента

Максимальное значение поперечной силы определяется по формуле:

/2.3.9/

Расчетное сечение приведено на рисунке 2.3.6. Опасные наклонные сечения начинаются в углу подрезки. Высота сечения здесь , ширина сечения равняется ширине ригеля b=b_p. Расчетная высота сечения, вводимая в расчет определяется, как . Значение а на первичном этапе можно принять равным а=20мм.

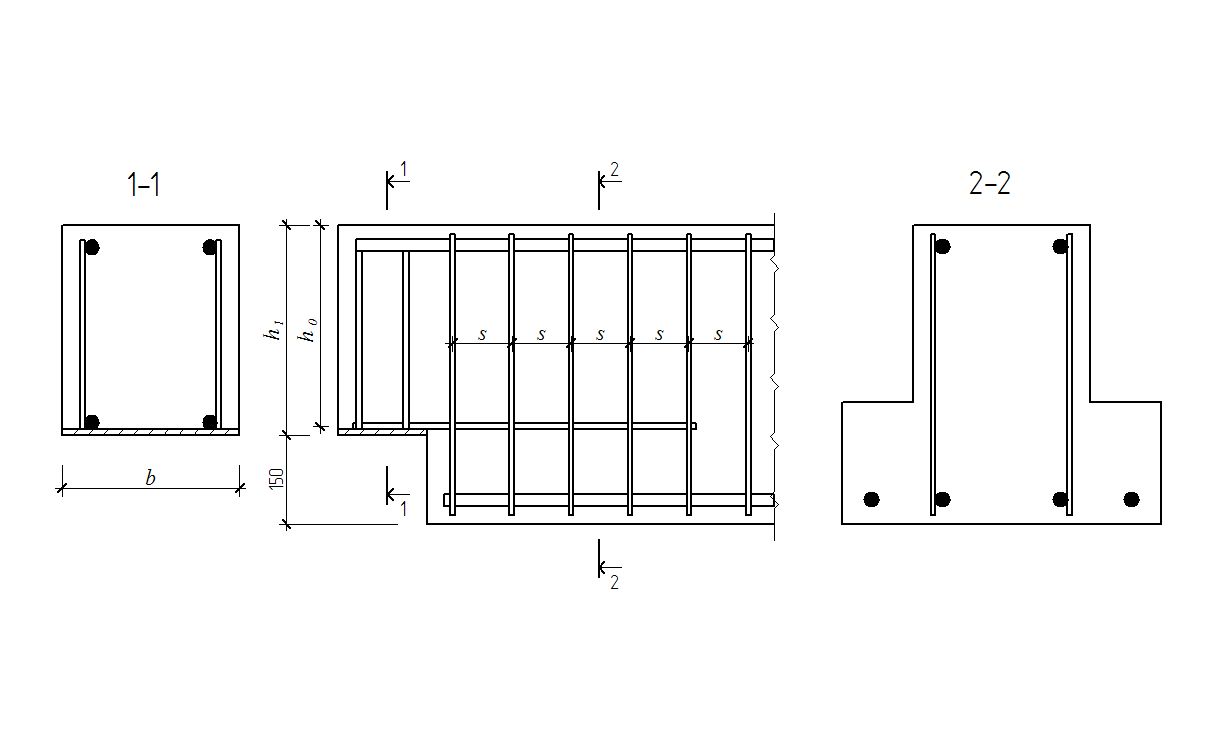
Рисунок 2.3.6 – К расчету ригеля по наклонному сечению

Далее расчет прочности ригеля по сечениям наклонным к продольной оси элемента при действии поперечной силы выполняется так же как и для плиты перекрытия (смотри п. 2.2.3).

2.3.3Расчет ригеля по наклонному сечению на изгибающий момент

Для обеспечения прочности в растянутой зоне в опорной зоне устанавливают дополнительную продольную арматуру диаметр которой определяют расчетом наклонных сечений на изгиб. Для надежного заанкеривания ее приваривают к опорной закладной пластине толщиной не менее 10 мм.

Расчет ригеля по наклонным сечениям на действие моментов (рисунок 2.3.7) производят из условия

/2.3.10/

где М - момент в наклонном сечении с длиной проекции с на продольную ось элемента, определяемый от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения (точка О), противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;

- момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка О);

- момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка О).

Момент определяют по формуле

, /2.3.11/

где - плечо внутренней пары сил, которое допускается принимать .

Момент для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле:

, /2.3.12/

где - усилие в поперечной арматуре, принимаемое равным ;

q_sw и с принимают те же, что и в предыдущем расчете;

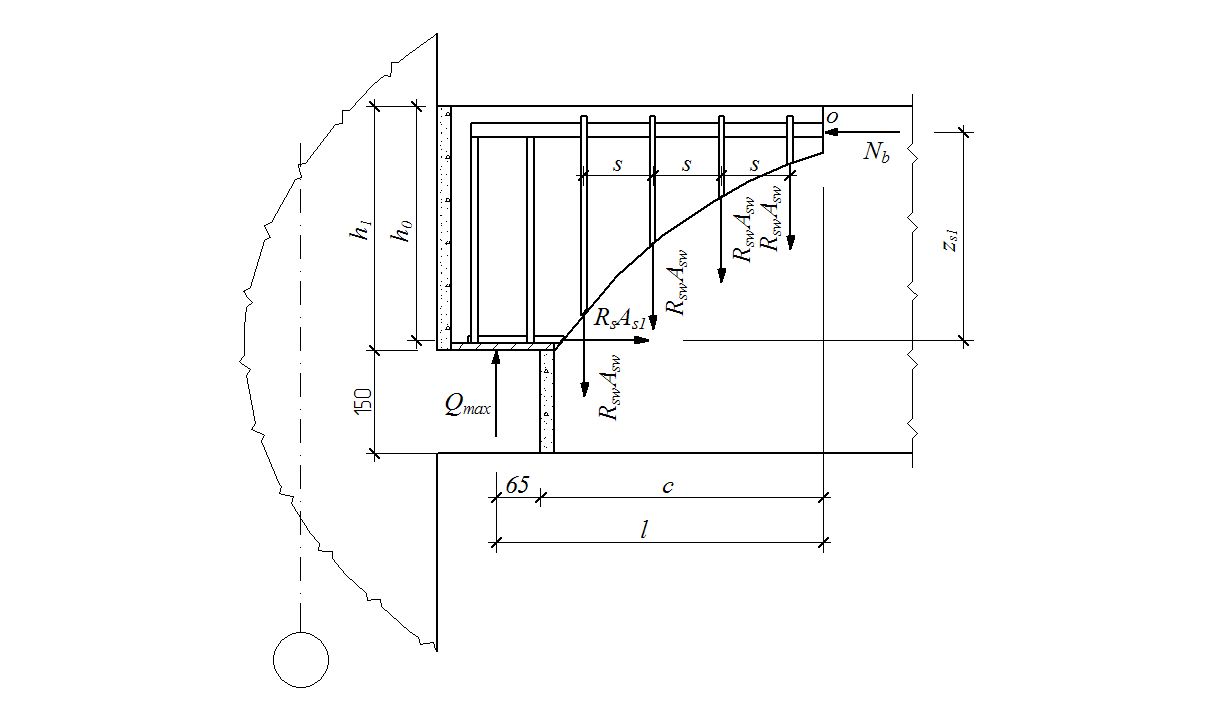
Рисунок 2.3.7 – К расчету ригеля по наклонному сечению на изгибающий момент

Допускается принимать значение момента для поперечной арматуры в предположении того, что с=h₀, тогда

. /2.3.13/

Главная задача в этом расчете определить требуемую площадь арматурного анкера с площадью арматуры A_s1.

С этой целью определим значение внешнего изгибающего момента действующего в опасном сечении по формуле:

, /2.3.14/

значение величины l – определяется по рисунку 4.7 при условии, что с=h₀.

Затем определяется значение момента для поперечной арматуры по формуле 4.20 или 4.21.

Из формулы 4.18 определим минимальное значение момента по формуле:

/2.3.15/

После чего можно определить требуемую площадь арматуры A_s1, исходя из формулы 4.19.

. /2.3.16/

По результатам расчета необходимо назначить диаметр арматуры при количестве стержней равном два.

Длина зоны анкеровки, на которую должны быть заведены стержни (то есть длина стержней) должна быть не менее , , 20×d_s, 250мм. Длина определяется по формуле:

, /2.3.17/

где - коэффициент, учитывающий влияние на длину анкеровки напряженного состояния бетона и арматуры и для растянутой арматуры периодического профиля принимается равным ;

, - площади поперечного сечения арматуры, соответственно требуемая по расчету и фактически установленная;

- базовая (основная) длина анкеровки, необходимая для передачи усилия в арматуре с полным расчетным сопротивлением R_s на бетон, определяют по формуле:

, /2.3.18/

где и - соответственно площадь поперечного сечения анкеруемого стержня арматуры и периметр его сечения, определяемые по номинальному диаметру стержня;

- расчетное сопротивление сцепления арматуры с бетоном, принимаемое равномерно распределенным по длине анкеровки и определяемое по формуле:

, /2.3.19/

здесь - расчетное сопротивление бетона осевому растяжению по первой группе предельных состояний;

- коэффициент, учитывающий влияние вида поверхности арматуры, принимаемый равным:

• 1,5 – для гладкой арматуры;

• 2 – для холоднодеформированной арматуры периодического профиля;

• 2,5 – для горячекатаной и термомеханически обработанной арматуры периодического профиля;

- коэффициент, учитывающий влияние размера диаметра арматуры, принимаемый равным:

• 1,0 - при диаметре арматуры d_s < 32 мм;

• 0,9 - при диаметре арматуры 36 и 40 мм.