2
1.Процесс интерполяции в MathCad
1.1.В-СПЛАЙН ИНТЕРПОЛЯЦИЯ
Представляет
интерес задача: т.е. задано известное
множество данных на поверхности, надо
найти задающую полигональную сетку для
В-сплайн поверхности, наилучшим образом
интерполирующей эти данные. Так как
границы поверхности, представляемой
этими данными, обычно известны, то здесь
будут рассматриваться только незамкнутые
В-сплайн поверхности. Разработка
аналогичного метода для замкнутых
поверхностей с помощью периодических
В-сплайн поверхностей не представляет
труда. Обсуждение ограничивается
топологически прямоугольными сетками,
т. е. данные умозрительно могут быть
представлены как находящиеся в точках
пересечения прямоугольной решетки. Эта
задача схематично изображена на рис.
6-49, где показана задающая полигональная
сетка размера
для
матрицы данных
.
Для того чтобы повысить эффективность
вычислений, были использованы известные
свойства бикубических В-сплайн
поверхностей. Применяемый нами метод
более прямолинеен, но имеет меньшую
вычислительную эффективность.
Заметим,
что
в
этом уравнении являются известными
точками на поверхности. Базисные функции
и
могут
быть определены для известного порядка
и известного числа вершин задающей
полигональной сетки в каждом параметрическом
направлении при условии, что известны
значения параметров
,
в
исходных точках.
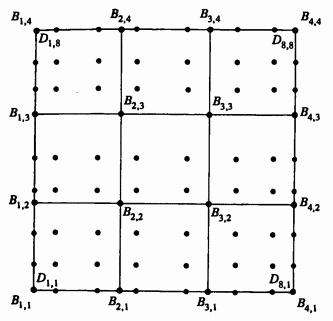
Рис. 1. Определение В-сплайн поверхности по известному набору данных.
В результате для исходной точки поверхности получим
,
где
для топологически прямоугольного
множества
данных
выполняются неравенства
и
.
Записав уравнения такого вида для всех
исходных точек, мы получим систему
уравнений. В матричном виде данный
результат записывается так:
,
где
.
Для топологически прямоугольных исходных
данных размера
матрица
является
матрицей
,
содержащей трехмерные координаты
исходных точек,
является
матрицей
трехмерных
координат искомых точек полигональной
сетки.
Если матрица квадратная, то задающая полигональная сетка находится с помощью обращения матрицы, т.е.
.
(6-83)
В
этом случае получившаяся поверхность
проходит через все исходные точки. Хотя
эта поверхность будет везде
,
гладка,
но она может быть неприемлема с точки
зрения пользователя.
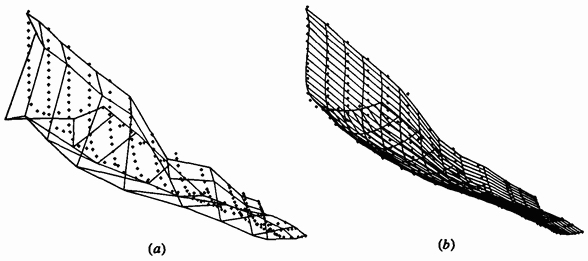
Рис. 2. Интерполяция В-сплайн поверхностью. (a) Исходные точки и интерполирующий характеристический многогранник; (b) исходные точки и сгенерированная поверхность.
Опыт показывает, что в общем случае, чем меньше точек задающей полигональной сетки, тем лучше выглядит поверхность.
Если не квадратная, то мы имеем избыточное количество исходных данных и решение может быть получено в некотором усредненном смысле. В частности, решение может быть получено в виде
.
(6-84)
Параметрические
значения
и
для
каждой исходной точки поверхности
получаются с помощью аппроксимации
длины хорды (см. разд. 5-11). Конкретнее,
для
исходных
точек значение параметра в
-й
точке в параметрическом направлении
равно
.
Аналогично
для
исходных
точек в параметрическом направлении
,
где
и
являются
максимальными значениями соответствующих
узловых векторов. На рис. 6-50а показаны
исходные данные и задающая полигональная
сетка, сгенерированная с помощью данного
метода. На рис. 6-50b изображена В-сплайн
поверхность, созданная по этой сетке.
Для интерполяции с помощью В-сплайн кривой данный метод не может привести к появлению точек или линий складок (разрывов первой или второй производной) в получаемой поверхности.
Отметим из рис. 2, что вершины задающей полигональной сетки, полученные из уравнения (1), расположены произвольным образом в пространстве. Это неудобно, если в дальнейшем поверхность предполагается модифицировать. Разработан итерационный метод, основанный на параметрических значениях , , в результате которого вершины сетки располагаются на плоскостях или вдоль кривых в трехмерном пространстве.