Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Южно-Уральский государственный университет»»

Факультет «Приборостроительный»

Кафедра «БИС»

Канонический метод структурного синтеза цифрового автомата.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОМУ ПРОЕКТУ

по дисциплине «ТЕОРИЯ АВТОМАТОВ».

ЮУрГУ–090900.2011.1894 ПЗ КР

Руководитель Парасич В.А. _______________2013 г.

Автор проекта студент группы ПС-255 Петров А.С. _______________2013 г.

Проект защищен с оценкой _____________________ _______________2013 г.

Челябинск 2013

ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Южно-Уральский государственный университет»»

Факультет «Приборостроительный»

Кафедра «БИС»

Специальность «090900»

ЗАДАНИЕ

на курсовой проект студента

Петрова Александра Сергеевича

Группа – ПС-255

Теория автоматов

Канонический метод структурного синтеза цифрового автомата

Срок сдачи студентом законченной работы _________________2013 г.

Перечень вопросов, подлежащих разработке:

На основе заданной совмещенной таблицы переходов/выходов спроектировать функциональную схему управляющего устройства

	u1	u3	u2	u2	u3

Элемент памяти – JK-триггер

Аннотация

В данной работе был рассмотрен канонический метод структурного синтеза цифрового автомата, элементом памяти которого является JK-триггер.

ОГЛАВЛЕНИЕ

Введение 4

1 Переход от JK-триггера к Т-триггеру 5

2 Каноническая структура цифрового автомата 8

3 Кодирование сигналов и состояний 9

4 Каноническая система уравнений 11

4.1 Система канонических уравнений для выходных сигналов 11

4.2 Система канонических уравнений для функций возбуждения 11

5 Минимизация системы канонических уравнений 14

5.1 Минимизация выходных сигналов 14

5.2 Минимизация функций возбуждения 15

5.3 Минимизированная каноническая система уравнений 17

6 Получение функциональной схемы автомата 17

7 Проверка функционирования управляющего устройства 20

Заключение 21

Библиографический список 22

Введение

Канонический метод структурного синтеза цифрового автомата является основным методом получения структурного автомата из абстрактной математической модели автомата. Целью структурного синтеза является построение схемы, реализующий автомат из логических элементов заданного типа. Если абстрактный автомат был лишь математической моделью дискретной системы, то в структурном автомате учитывается структура входных и выходных сигналов автомата, его внутреннее устройство на уровне структурных схем, а так же рассматриваются вопросы обеспечения устойчивой работы автомата.

1 Переход от jk-триггера к т-триггеру

Составим таблицу функционирования переходов/выходов так, чтобы можно было свободно перемещаться из одного состояния в другое (таблица 1.1).

Таблица 1.1

	а1	а2	а3
q1	а2/10	а1/01	а3/00
q2	а1/01	а2/10	a2/11
q3	а3/01	а3/10	а1/11

Закодируем данные состояния и сигналы (таблица 1.2):

Таблица 1.2

q1	00
q2	01
q3	10

Поскольку в исходной таблице не используется сигнал 11, то закодируем состояния так (таблица 1.3).

Таблица 1.3

а1	01
а2	10
а3	11

Составляем таблицу кодированных состояний (таблица 1.4):

Таблица 1.4

	01	10	11
00	10	01	11
01	01	10	10
10	11	11	01

Поскольку в исходной таблице отсутствует входной сигнал 11, то при данном состоянии и входе у нас должен быть предупреждающий сигнал.

Соответственно схема будет следующей (рисунок 1.1).

TT TT TT

Рисунок 1.1 – Схема системы

Выход на рисунке 1.1 справа переводит ее в следующее состояние, выход снизу используется при некорректном вводе.

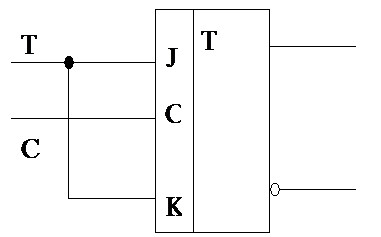
Функциональная схема перехода от JK-триггера к Т-триггеру представлена на рисунке 1.2.

Рисунок 1.2 – Переход от JK-триггера к Т-триггеру

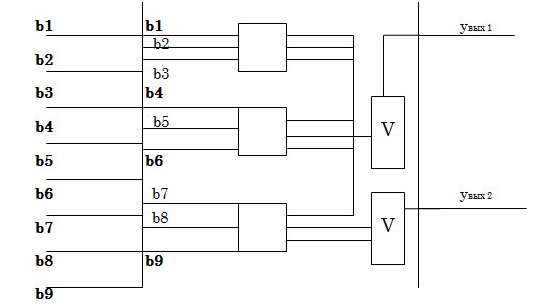
Далее проектирование ведем на базе Т-триггеров. Полная схема представлена на рисунке 1.3.

TT TT TT

Рисунок 1.3 – Полная схема перехода